
Next: Least Square Regression Up: Main:
Previous: 2.3.1 Gregory-Newton Forward Difference
If the data size is big then the divided difference table will be
too long. Suppose the desired intermediate value
![]() at which one needs to estimate the function
at which one needs to estimate the function
![]() falls towards the end or say in the
second half of the data set then it may be better to start the
estimation process from the last data set point. For this we need
to use backward-differences and backward difference table.
falls towards the end or say in the
second half of the data set then it may be better to start the
estimation process from the last data set point. For this we need
to use backward-differences and backward difference table.
Let
us first define backward differences and generate backward
difference table, say for the data set
![]()
First order backward difference
![]() is defined as:
is defined as:
| (11.1) |
| (11.2) |
| (11.3) |
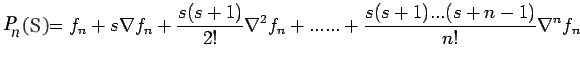 |
(12) |
Where
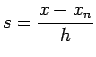
For constructing ![]() as given in
as given in ![]() it will be easier if we first
generate backward-difference table. The backward difference table
for the data
it will be easier if we first
generate backward-difference table. The backward difference table
for the data
![]() is given below:
is given below:

The rounded differences appear in Eqn (12)
Newton Backward Difference Table:
Now let us
apply Newton Backward difference approach to the second example
solved earlier following the Newton forward difference approach
i.e.
Example:
Given the following data estimate ![]() using Newton-Gregory backward difference interpolation polynomial:
using Newton-Gregory backward difference interpolation polynomial:
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 4 | 5 | |
| 1 | 2 | 4 | 8 | 16 | 32 |
![]()
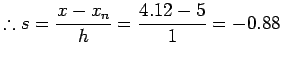
![]() Newton Backward Difference polynomial
Newton Backward Difference polynomial ![]() is
given by
is
given by
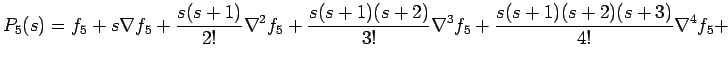 |
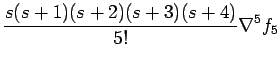 |
Let us first generate backward difference table:
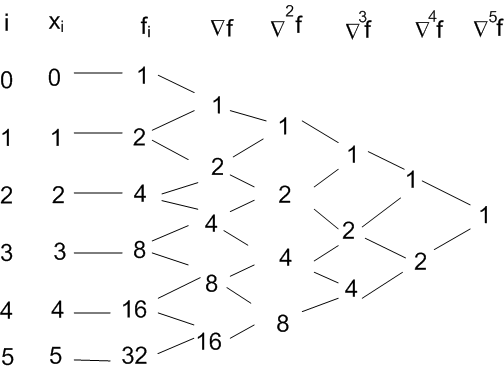
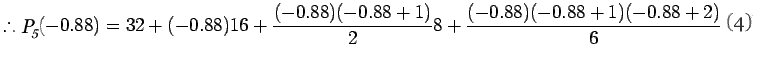 |
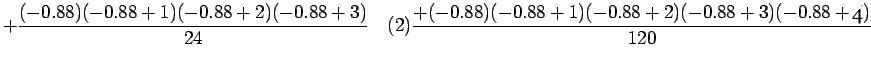 |
.1 |
=17.39135 (13.5)
Now for comparison with the earlier solution i.e. the one obtained
by forward Newton Divided Difference approach we may look at the
above solution in stages similar to that provided earlier i.e.
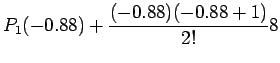 |
|||
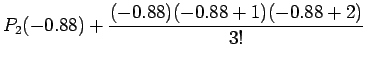 |
|||
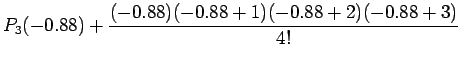 |
|||
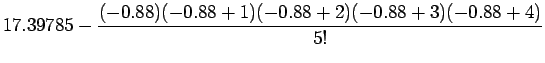 |
|||
Now one may note from (13.2) and (10a.2) that it is definitely
advantageous of use backward difference approach here, as in
exactly the same number of steps we are relatively more close to
the approximate solution.
Exercise:
1) Given
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
f(x) |
1 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
Estimate f(7.5) using Newton-Gregory Backward difference
interpolation formula.
2) Given
x |
1.0 | 2.0 | 3.0 | 4.0 |
ln x |
0.0 | 0.6931 | 1.0986 | 1.3863 |
Estimate ln(3.5) using Newton-Gregory Backward difference interpolation formula.