


Next: Newton Interpolation polynomial:
Up: Main:Previous: Introduction:
Interpolation
Let us suppose that the given
data points
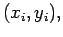
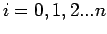
is coming from a
function
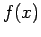
. Let us assume that this function
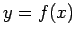
takes
the values
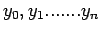
at
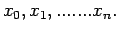
Since there are
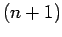
data points
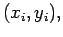
we can represent the function
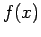
by a
polynomial of degree
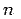
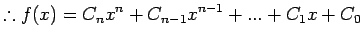 |
(1) |
As we have assumed that
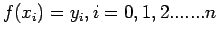 i.e. the
function
i.e. the
function 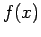 passes through
passes through
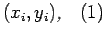 can be
rewritten as:
can be
rewritten as:
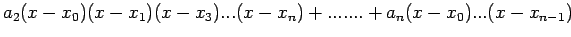 |
(2) |
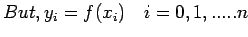 |
(3) |
Using (3) for i=0, in (2) we get
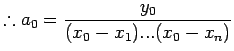 |
(4.1) |
For 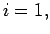 we get
we get
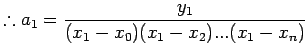 |
(4.2) |
Similarly for
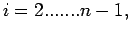 we get
and for
we get
and for 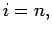 we get
we get
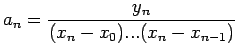 |
(4.3) |
Using (4.1)-(4.3) in (2) we get
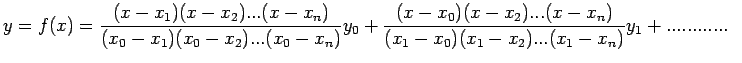 |
(5) |
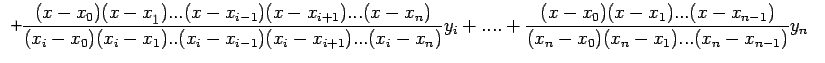 |
(6) |
(5) can be rewritten in a compact form as:
where
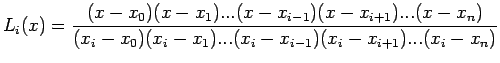 |
(7.2) |
It can be easily noted that
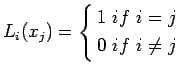 |
7.3 |
Let us introduce the product notation as :
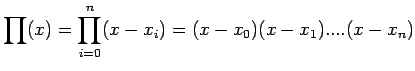 |
(8.1) |
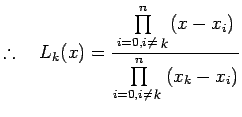 |
(8.2) |
Therefore, Lagrange interpolation polynomial of degree n can be
written as
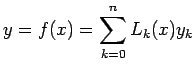 |
(9) |
Example 1:
Given the following data table, construct the
Lagrange interpolation
polynomial 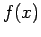 , to fit the data and find
, to fit the data and find 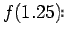
| i |
0 |
1 |
2 |
3 |
 |
0 |
1 |
2 |
3 |
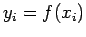 |
1 |
2.25 |
3.75 |
4.25 |
Solution:
Here 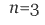 .
.
 Lagrange interpolation polynomial is given by
Lagrange interpolation polynomial is given by
Example 2:
Given the following data table, construct the
Lagrange interpolation polynomial f(x), to fit the data and find 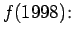
| i |
0 |
1 |
2 |
3 |
4 |
5 |
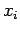 |
1980 |
1985 |
1990 |
1995 |
2000 |
2005 |
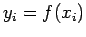 |
440 |
510 |
525 |
571 |
500 |
600 |
Solution:
Here
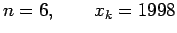
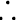 Lagrange interpolation polynomial is given by
Lagrange interpolation polynomial is given by
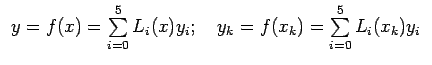


Next: Newton Interpolation polynomial:Up: Main:
Previous: Introduction:

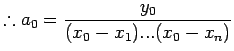
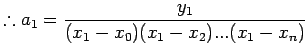
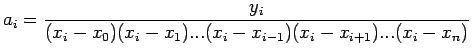
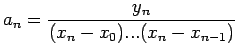
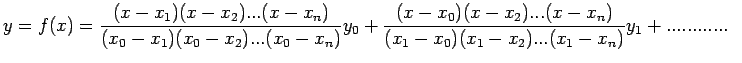
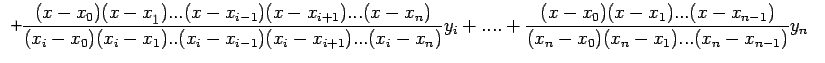
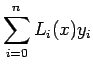

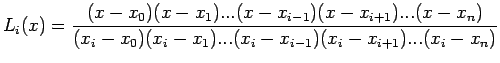
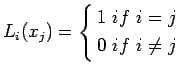
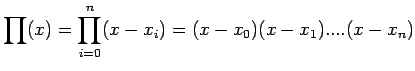
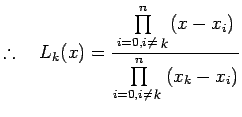
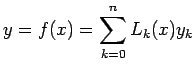
![]() , to fit the data and find
, to fit the data and find ![]()
![]() .
.
![]() Lagrange interpolation polynomial is given by
Lagrange interpolation polynomial is given by
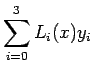
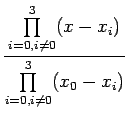
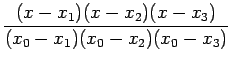
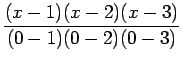
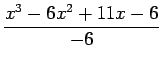
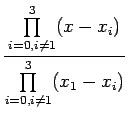
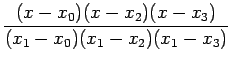
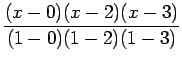
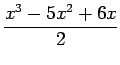
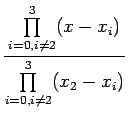
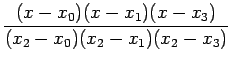
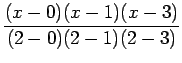
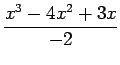
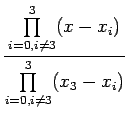
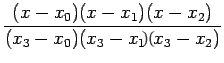
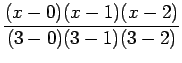
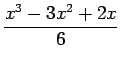
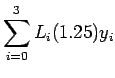
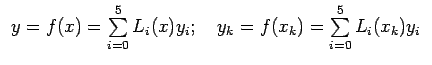
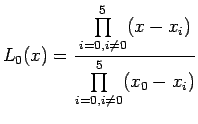
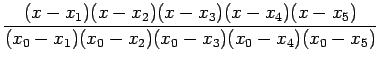
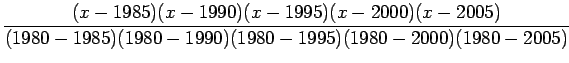
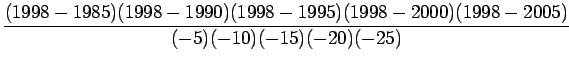
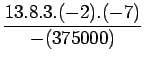
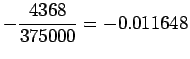
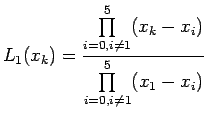
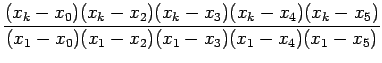
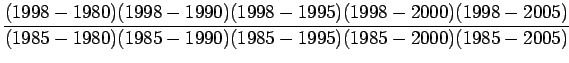
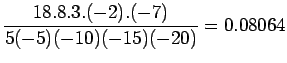
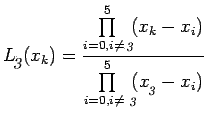
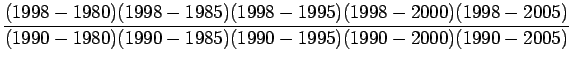
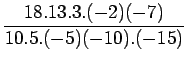
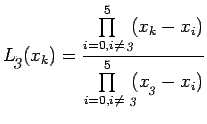
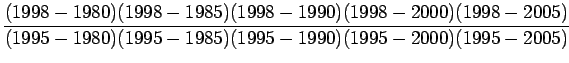
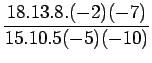
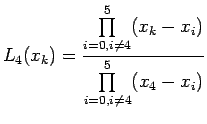
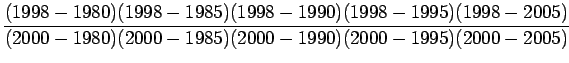

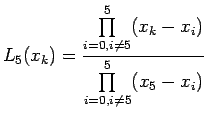
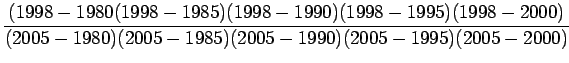
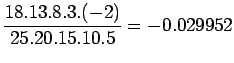
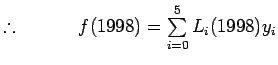
![]()
![]()
![]() . Suppose we are interested in evaluating
. Suppose we are interested in evaluating ![]() at some
intermediate point
at some
intermediate point ![]() to a desired level of accuracy. Directly
using the entire data set of size n may not only be
computationally economical but may also turn out to be redundant.
Naturally one would like to use an interpolating polynomial of optimal
degree. Since this is not known apriori, one may start with
to a desired level of accuracy. Directly
using the entire data set of size n may not only be
computationally economical but may also turn out to be redundant.
Naturally one would like to use an interpolating polynomial of optimal
degree. Since this is not known apriori, one may start with ![]() and if it was enough then move onto
and if it was enough then move onto ![]() and so
on i.e. slowly increase the no. of the interpolating points (or)
data points
and so
on i.e. slowly increase the no. of the interpolating points (or)
data points
![]() so that
so that
![]() will be
close to
will be
close to ![]() . In this context the biggest disadvantage with
Lagrange Interpolation is that we cannot use the work that has
already been done i.e. we cannot make use of
. In this context the biggest disadvantage with
Lagrange Interpolation is that we cannot use the work that has
already been done i.e. we cannot make use of
![]() while
evaluating
while
evaluating ![]() . With the addition of each new data point,
calculations have to be repeated. Newton Interpolation polynomial
overcomes this drawback.
. With the addition of each new data point,
calculations have to be repeated. Newton Interpolation polynomial
overcomes this drawback.
![]() ,
, ![]()
![]()