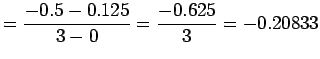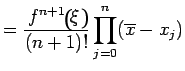Next: (2.2.2)Newton Divided Difference Table:
Up: Curve Fitting : Interpolation,
Previous: Lagrange Interpolation:
Suppose that we are given a data set
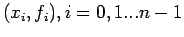 .
Let us assume that these are interpolating points of Newton form
of interpolating polynomial
.
Let us assume that these are interpolating points of Newton form
of interpolating polynomial 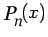 of degree
of degree 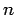 i.e
i.e
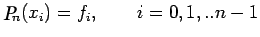 |
(1) |
The Newton form of the interpolating polynomial 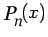 is
given by
is
given by
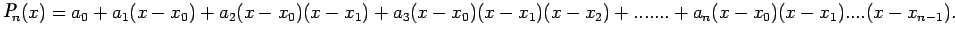 |
(2) |
For i=0, from (1)-(2) we get
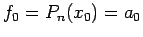 |
(3.1) |
For 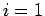 from (1)-(2) we get
from (1)-(2) we get
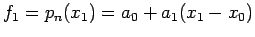
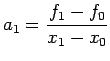 |
(3.2) |
For i=2 from(1)-(2) We get
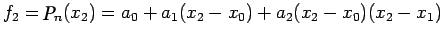
using (3.1)-(3.2), we get
![$\displaystyle a_{2}=\frac{[(f_{2}-f_{1})/(x_{2}-x_{1})]-[(f_{1}-f_{0})/(x_{1}-x_{0})]}{(x_{2}-x_{0})}$](img121.png) |
(3.3) |
Similarly we can find
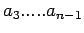 . To express
. To express
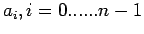 in a compact manner let us first define the
following notation called divided differences:
in a compact manner let us first define the
following notation called divided differences:
![$\displaystyle f[x_{k}]=f_{k}$](img124.png) |
(4.1) |
![$\displaystyle \hspace{0.5in}f[x_{k},x_{k+1}]=\frac{f[x_{k+1}]-f[x_{k}]}{x_{k+1}-x_{k}}$](img125.png) |
(4.2) |
![$\displaystyle \hspace{0.9in}f[x_{k},x_{k+1},x_{k+2}]=\frac{f[x_{k+1},x_{k+2}]-f[x_{k},x_{k+1}]}{x_{k+2}-x_{k}}$](img126.png) |
(4.3) |
![$\displaystyle \hspace{0.5in}f[x_{k},x_{k-1}....x_{i},x_{i+1}]=\frac{f[x_{k+1}...x_{i+1}]-f[x_{k}...x_{i}]}{x_{i+1}-x_{k}}$](img127.png) |
(4.4) |
Now the co-efficients
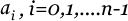 can be expressed in
terms of divided differences as fellows:
can be expressed in
terms of divided differences as fellows:
![$\displaystyle a_{0}=f_{0}=f[x_{0}]$](img129.png) |
(5.1) |
![$\displaystyle a_{1}=\frac{f_{1}-f_{0}}{x_{1}-x_{0}}=f[x_{1},x_{0}]$](img130.png) |
(5.2) |
![$\displaystyle =f[x_{0},x_{1},x_{2}]$](img132.png) |
(5.3) |
![$\displaystyle a_{n}=f[x_{0},x_{1}...x_{n}]$](img133.png) |
(5.4) |
Note that 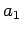 is called as the first divided difference,
is called as the first divided difference,
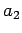 as the second divided difference and so on. Now the
polynomial (2) can be rewritten as:
as the second divided difference and so on. Now the
polynomial (2) can be rewritten as:
i.e.![$\displaystyle \hspace{1in}p_{n}(x)=\sum\limits_{k=0}^{n}f[x_{0}......x_{k}]\prod\limits_{i=0}^{k-1}(x-x_{i})$](img137.png) |
(6) |
This is called as Newton's Divided Difference
interpolation polynomial.
Example:
Given the following data table, evaluate 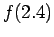 using
using 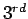 order Newton's Divided Difference interpolation polynomial.
order Newton's Divided Difference interpolation polynomial.
| i |
0 |
1 |
2 |
3 |
4 |
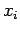 |
0 |
1 |
2 |
3 |
4 |
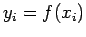 |
1 |
2.25 |
3.75 |
4.25 |
5.81 |
Solution:
Here 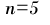 . For constructing
. For constructing 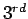 order
Newton Divided Difference polynomial we need only four points. Let
us use the first four points. The
order
Newton Divided Difference polynomial we need only four points. Let
us use the first four points. The 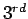 Newton Divided
Difference polynomial is given by:
Newton Divided
Difference polynomial is given by:
![$ p_{3}(x)=\sum\limits_{k=0}^{3}a_{k}\prod\limits_{j=0}^{k-1}(x-x_{j})\\ =\sum\limits_{k=0}^{3}f[x_{0}...x_{k}]\prod\limits_{j=0}^{k-1}(x-x_{j})$](img141.png)
![$ =f[x_{0}]+f[x_{0},x_{1}](x-x_{0})+
f[x_{0},x_{1},x_{2}](x-x_{0})(x-x_{1})+
f[x_{0},x_{1},x_{2},x_{3}](x-x_{0})(x-x_{1})(x-x_{3})$](img142.png)
![% latex2html id marker 2479
$ \therefore a_{0}=f[x_{0}]=1$](img143.png)
![$ a_{1}=f[x_{0},x_{1}]=\displaystyle
{\frac{f(x_{1})-f(x_{0})}{(x_{1}-x_{0})}}=\frac{2.25-1}{1-0}=1.25$](img144.png)
![$ \displaystyle
{f[x_{1}x_{2}]=\frac{f[x_{2}]-f[x_{1}]}{x_{2}-x_{1}}=\frac{3.75-2.25}{2-1}=1.5}$](img145.png)
![% latex2html id marker 2485
$ \displaystyle{\therefore
a_{2}=f[x_{0},x_{1},x_{2}]=\frac{f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}=\frac{1.5-1.25}{2-0}=0.125}$](img146.png)
![$ \displaystyle{f[x_{2},x_{3}]=\frac{f[x_{3}]-f[x_{2}]}{x_{3}-x_{2}}=\frac{4.25-3.75}{3-2}=\frac{0.5}{1}=0.5}$](img147.png)
![$ \displaystyle{f[x_{1},x_{2},x_{3}]=\frac{f[x_{2},x_{3}]-f[x_{1},x_{2}]}{x_{3}-x_{1}}=\frac{0.5-1.5}{3-1}=-0.5}$](img148.png)
![% latex2html id marker 2491
$ \displaystyle{\therefore
a_{3}=f[x_{0},x_{1},x_{2},x_{3}]=\frac{f[x_{1},x_{2},x_{3}]-f[x_{0},x_{1},x_{2}]}{x_{3}-x_{0}}}$](img149.png)
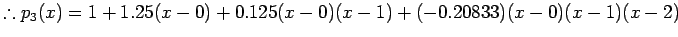
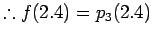
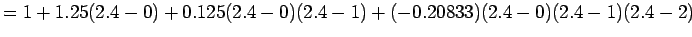
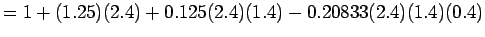
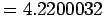
In this example it may be noted that for calculating the 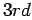 order polynomial, we first start with
order polynomial, we first start with
![$ P_{0}=f[x_{0}]=1$](img157.png) . To it we
add
. To it we
add
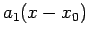 to get
to get 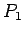 and to
and to 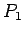 we add
we add
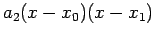 to get
to get 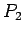 . Finally on adding
. Finally on adding
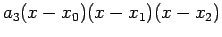 to
to 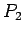 we get
we get 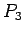 .
.
Some remarks on the Error in the interpolation
approach:
Suppose that the given data points
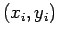 ,
, 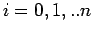 correspond to a real valued function
correspond to a real valued function 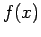 defined on the
internal
defined on the
internal ![$ I=[a,b]$](img166.png) . Let
. Let 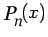 be the interpolating polynomial
of degree
be the interpolating polynomial
of degree 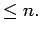
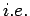
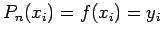
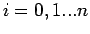 . Then the interpolation error
. Then the interpolation error 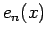 due to
interpolation by
due to
interpolation by 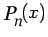 is given by
is given by
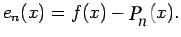 |
(6.2) |
An estimate of the error is provided in the following theorem.
Theorem: Let 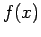 be a real-valued function define on
be a real-valued function define on
![$ [a,b]$](img173.png) and
and 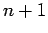 times differentiable on
times differentiable on 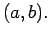 If
If 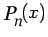 is the polynomial of degree
is the polynomial of degree 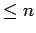 which interpolates
which interpolates 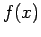 at
the (n+1) distinct points
at
the (n+1) distinct points
![$ x_{0}..x_{n}\epsilon[a,b]$](img177.png) , then for
all
, then for
all
![$ \overline{x}\epsilon[a,b]$](img178.png) , there exits
, there exits
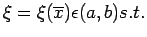
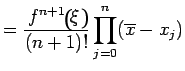 |
(6.3) |
Note:
i)
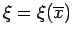 i.e.
i.e. 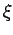 depends on
the
point
depends on
the
point
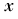 at which the error estimate is required.
at which the error estimate is required.
ii) since
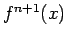 i.e.
i.e.
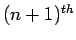 derivative is seldom
known the error formula
derivative is seldom
known the error formula 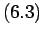 in the above theorem is of limited
practical value. But when a bound on
in the above theorem is of limited
practical value. But when a bound on
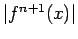 is known over
the entire internal
is known over
the entire internal ![$ [a,b]$](img173.png) , then the formula
, then the formula 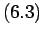 may be used
to get a bound on the interpolation error.
may be used
to get a bound on the interpolation error.



Next: (2.2.2)Newton Divided Difference Table:
Up: Curve Fitting : Interpolation,
Previous: Lagrange Interpolation:
root
2006-02-14
![]() .
Let us assume that these are interpolating points of Newton form
of interpolating polynomial
.
Let us assume that these are interpolating points of Newton form
of interpolating polynomial ![]() of degree
of degree ![]() i.e
i.e
![]()
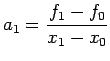
![]()
![$\displaystyle a_{2}=\frac{[(f_{2}-f_{1})/(x_{2}-x_{1})]-[(f_{1}-f_{0})/(x_{1}-x_{0})]}{(x_{2}-x_{0})}$](img121.png)
![$\displaystyle \hspace{0.5in}f[x_{k},x_{k+1}]=\frac{f[x_{k+1}]-f[x_{k}]}{x_{k+1}-x_{k}}$](img125.png)
![$\displaystyle \hspace{0.9in}f[x_{k},x_{k+1},x_{k+2}]=\frac{f[x_{k+1},x_{k+2}]-f[x_{k},x_{k+1}]}{x_{k+2}-x_{k}}$](img126.png)
![$\displaystyle \hspace{0.5in}f[x_{k},x_{k-1}....x_{i},x_{i+1}]=\frac{f[x_{k+1}...x_{i+1}]-f[x_{k}...x_{i}]}{x_{i+1}-x_{k}}$](img127.png)
![$\displaystyle a_{1}=\frac{f_{1}-f_{0}}{x_{1}-x_{0}}=f[x_{1},x_{0}]$](img130.png)
![$\displaystyle a_{2}=\displaystyle
{\frac{\frac{f_{2}-f_{1}}{x_{2}-x_{1}}-\frac{...
...}{x_{1}-x_{0}}}{x_{2}-x_{0}}}=\frac{f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}$](img131.png)
![$\displaystyle \hspace{1in}p_{n}(x)=\sum\limits_{k=0}^{n}f[x_{0}......x_{k}]\prod\limits_{i=0}^{k-1}(x-x_{i})$](img137.png)
![$ p_{3}(x)=\sum\limits_{k=0}^{3}a_{k}\prod\limits_{j=0}^{k-1}(x-x_{j})\\ =\sum\limits_{k=0}^{3}f[x_{0}...x_{k}]\prod\limits_{j=0}^{k-1}(x-x_{j})$](img141.png)
![$ a_{1}=f[x_{0},x_{1}]=\displaystyle
{\frac{f(x_{1})-f(x_{0})}{(x_{1}-x_{0})}}=\frac{2.25-1}{1-0}=1.25$](img144.png)
![$ \displaystyle
{f[x_{1}x_{2}]=\frac{f[x_{2}]-f[x_{1}]}{x_{2}-x_{1}}=\frac{3.75-2.25}{2-1}=1.5}$](img145.png)
![% latex2html id marker 2485
$ \displaystyle{\therefore
a_{2}=f[x_{0},x_{1},x_{2}]=\frac{f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}=\frac{1.5-1.25}{2-0}=0.125}$](img146.png)
![$ \displaystyle{f[x_{2},x_{3}]=\frac{f[x_{3}]-f[x_{2}]}{x_{3}-x_{2}}=\frac{4.25-3.75}{3-2}=\frac{0.5}{1}=0.5}$](img147.png)
![$ \displaystyle{f[x_{1},x_{2},x_{3}]=\frac{f[x_{2},x_{3}]-f[x_{1},x_{2}]}{x_{3}-x_{1}}=\frac{0.5-1.5}{3-1}=-0.5}$](img148.png)
![% latex2html id marker 2491
$ \displaystyle{\therefore
a_{3}=f[x_{0},x_{1},x_{2},x_{3}]=\frac{f[x_{1},x_{2},x_{3}]-f[x_{0},x_{1},x_{2}]}{x_{3}-x_{0}}}$](img149.png)