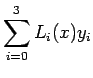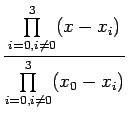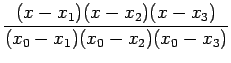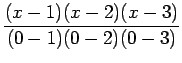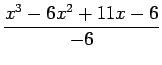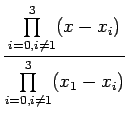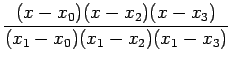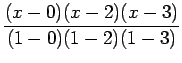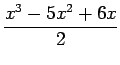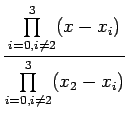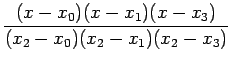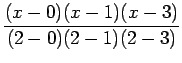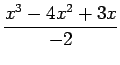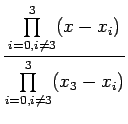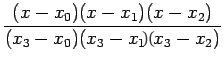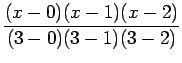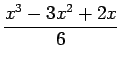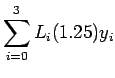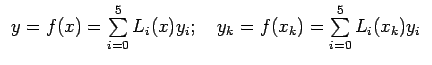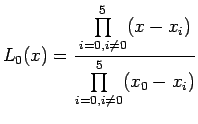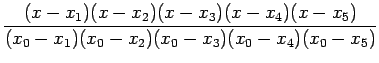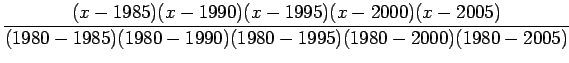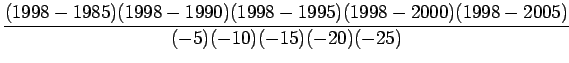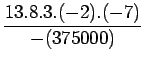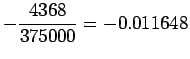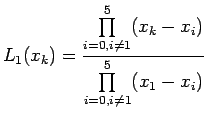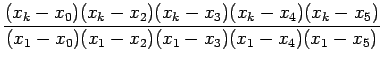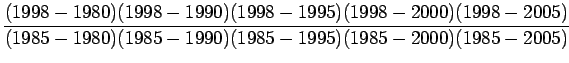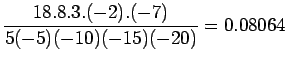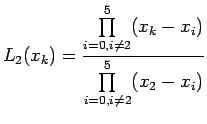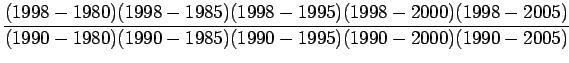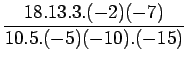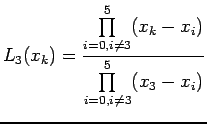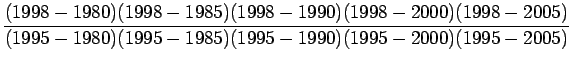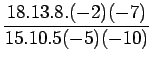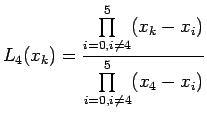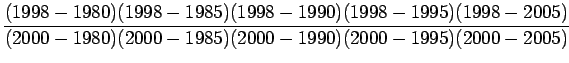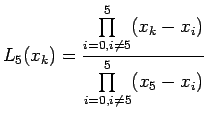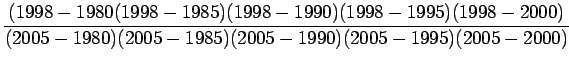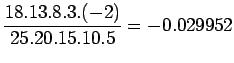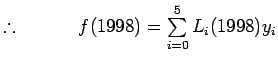Let us suppose that the given
data points
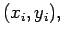
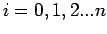
is coming from a
function
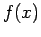
. Let us assume that this function
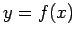
takes
the values
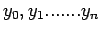
at
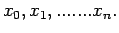
Since there are
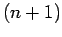
data points
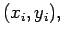
we can represent the function
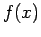
by a
polynomial of degree
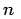
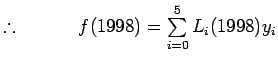
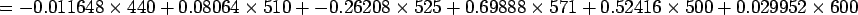
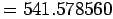 Note:
Note: Given a set of data points
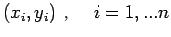
. Suppose we are interested in evaluating
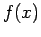
at some
intermediate point
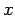
to a desired level of accuracy. Directly
using the entire data set of size n may not only be
computationally economical but may also turn out to be redundant.
Naturally one would like to use a interpolating polynomial of apt
degree. Since this is not known a priori, one may start with
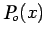
and if it was enough then move onto
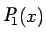
and so
on i.e. slowly increase the no. of the interpolating points (or)
data points
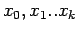
so that
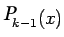
will be
close to
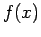
. In this context the biggest disadvantage with
Lagrange Interpolation is that we cannot use the work that has
already been done i.e. we cannot make use of
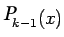
while
evaluating
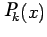
. With the addition each new data point,
calculations have to be repeated. Newton Interpolation polynomial
overcomes this drawback.
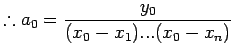
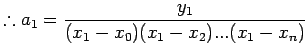
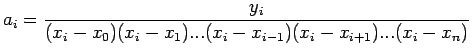
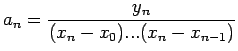
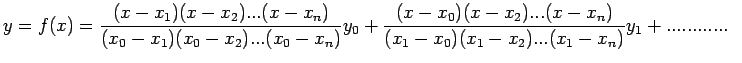
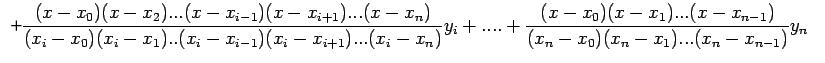
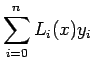

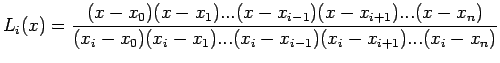
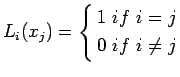
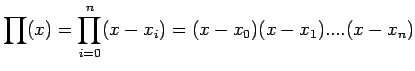
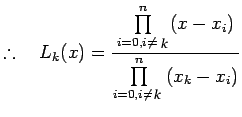
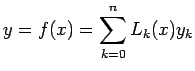
![]() .
.
![]() Lagrange interpolation polynomial is given by
Lagrange interpolation polynomial is given by