
Next: Nonlinear Regression Up: Main Previous:Least Squares Regression
Least -Squares Regression ...(continued)
Remarks:
(1) Experimental data may not be always linear. One may be
interested in fitting either a curve of the form ![]()
![]() or
or ![]()
![]() However, both of these forms can be
linearized by taking logarithms on both the sides. Let
us look at the details:
However, both of these forms can be
linearized by taking logarithms on both the sides. Let
us look at the details:
![]()
On taking logarithms on both the sides we get:
![]()
Say
![]()
Using (3) in (2) we get
![]()
which is linear in ![]() .
.
![]()
On taking logarithms we get
![]()
Say
![]()
![]() we get
we get
![]()
which is linear in ![]()
Example: By the method of least square fit a curve of the form
![]() to the following data:
to the following data:
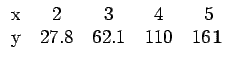
Solution.
Consider
![]()
On taking logarithm on both the sides we get
![]()
Say ![]()
Using (3) in (2) we get
![]()
Data in modified variables ![]()

Normal equations corresponding to the straight line fit (4) are:
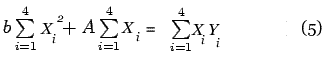
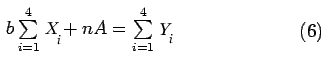
From the modified data we get

![]() normal equations take the form:
normal equations take the form:
![]()
![]()
On solving for ![]() we obtain,
we obtain,
![]()
![]()
![]() .
.
![]() The desired curve is
The desired curve is
![]()
Least Square fit of a parabola
Given a data set of n observations
![]() ,
, ![]() of an
experiment .Now we try to fit a best possible parabola
of an
experiment .Now we try to fit a best possible parabola
![]()
following the principle of least square. Finding the appropriate
parabola amounts to determining the constants ![]() that
minimize the sum of the squares of the residuals
that
minimize the sum of the squares of the residuals
![]() given by
given by
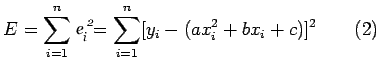
The necessary condition for E to be minimum is
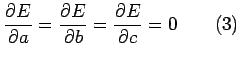
Now the condition
![]() yields
yields
=0$](img45.png)
i.e
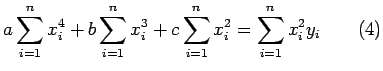
Similarly
![]() yields
yields
![$\displaystyle \frac{\partial E}{\partial
b}=-\sum\limits_{i=1}^{n}2[y_{i}-(ax^{2}_{i}+bx_{i}+c)]x_{i}=0$](img48.png)
i.e 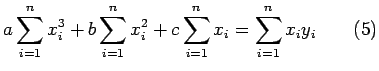
Finally
![]() yields
yields
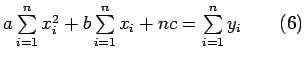
Equations (4), (5) and (6) are called as normal equations whose solution yields the values of the constants a, b and c and thus the desired parabola.
Example: Given the following data from an experimental observation
| y: | 9.4 | 11.8 | 14.7 | 18.0 | 23.0 | |
| x: | 1.0 | 1.6 | 2.5 | 4.0 | 6.0 |
fit a parabola in the form
![]() following the principle
of least square.
following the principle
of least square.
Solution) Here ![]()
The normal equations for finding a parabolic fit are:
|
(1) |
|
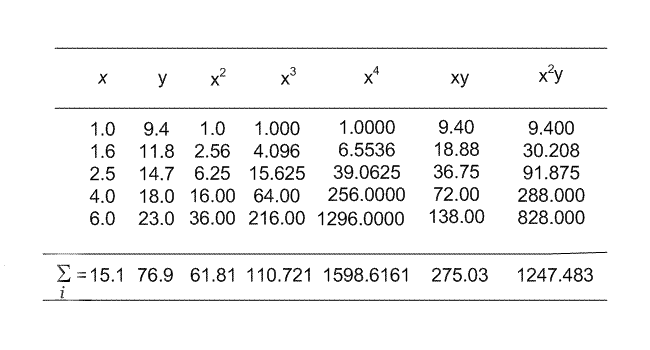
![]() The normal equations are:
The normal equations are:
| (2) | |
On Solving (2) for ![]() we get
we get
![]()
![]()
![]()
Next: Nonlinear Regression Up: Main Previous:Least Squares Regression