Introduction

Legendre Equation plays a vital role in many problems of mathematical Physics and in the theory of quadratures (as applied to Numerical Integration).

DEFINITION 9.4.1 The equation

$\displaystyle (1 - x^2) y^{\prime\prime} - 2 x y^\prime + p (p+1) y = 0, \; -1 < x < 1$

(9.4.1)

where $p \in {\mathbb{R}},$ is called a LEGENDRE EQUATION of order

Equation (9.4.1) was studied by Legendre and hence the name Legendre Equation.

Equation (9.4.1) may be rewritten as

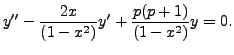
$\displaystyle y^{\prime\prime} - \frac{2 x}{(1 - x^2)} y^\prime + \frac{p (p+1)}{(1 - x^2)} y = 0.$

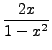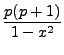The functions $\displaystyle\frac{ 2 x}{1 - x^2}$ and $\displaystyle\frac{p(p+1)}{1 - x^2}$ are analytic around

(since they have power series expressions with centre at

and with

as the radius of convergence). By Theorem 9.3.1, a solution

of (9.4.1) admits a power series solution (with centre at

) with radius of convergence

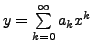Let us assume that $y = \sum\limits_{k=0}^\infty a_k x^k$ is a solution of (9.4.1). We have to find the value of

's. Substituting the expression for

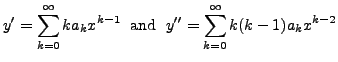
$\displaystyle y^\prime = \sum\limits_{k=0}^\infty k a_k x^{k-1} \; {\mbox{ and }} \; y^{\prime\prime} = \sum\limits_{k=0}^\infty k(k-1) a_k x^{k-2}$

in Equation (9.4.1), we get

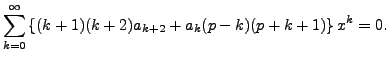
$\displaystyle \sum_{k=0}^\infty \left\{ (k+1)(k+2) a_{k+2} + a_k (p-k)(p+k+1) \right\} x^k = 0.$

Hence, for $k = 0, 1, 2, \ldots$

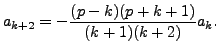
$\displaystyle a_{k+2} = - \frac{(p-k)(p+k+1)}{(k+1)(k+2)} a_k.$

It now follows that

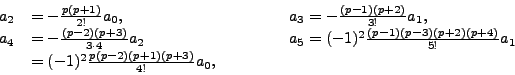
$\begin{displaymath}\begin{array}{lll} a_2 &= - \frac{p(p+1)}{2!}a_0, & \hspace{... ..._1 \\ &= (-1)^2 \frac{p(p-2)(p+1)(p+3)}{4!} a_0, & \end{array}\end{displaymath}$

etc. In general,

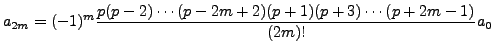
$\displaystyle a_{2m} = (-1)^m \frac{p(p-2)\cdots(p-2m+2) (p+1) (p+3) \cdots (p+2m -1)}{(2m)!} a_0$

and

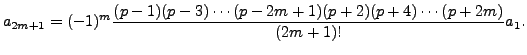
$\displaystyle a_{2m+1} = (-1)^m \frac{(p-1)(p-3)\cdots(p-2m+1) (p+2) (p+4) \cdots (p+2m)}{(2m+1)!} a_1.$

It turns out that both $ a_0$

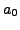and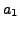

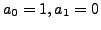are arbitrary. So, by choosing $ a_0 = 1, a_1 = 0$

and

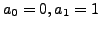in the above expressions, we have the following two solutions of the Legendre Equation (9.4.1), namely,

$\displaystyle y_1 = 1 - \frac{p(p+1)}{2!} x^2 + \cdots + (-1)^m \frac{(p-2m+2)\cdots (p+2m-1)}{(2m)!} x^{2m} + \cdots$

(9.4.2)

and

$\displaystyle y_2 = x - \frac{(p-1)(p+2)}{3!} x^3 + \cdots + (-1)^m \frac{(p-2m+1) \cdots (p+2m)}{(2m+1)!} x^{2m+1} + \cdots.$

(9.4.3)

Remark 9.4.2 and are two linearly independent solutions of the Legendre Equation (9.4.1). It now follows that the general solution of (9.4.1) is

$\displaystyle y = c_1 y_1 + c_2 y_2$

(9.4.4)

where and are arbitrary real numbers.

A K Lal 2007-09-12