Next: Legendre Equations and Legendre Up: Solutions Based on Power Previous: Solutions in terms of Contents
Earlier, we saw a few properties of a power series and some uses also. Presently, we inquire the question, namely, whether an equation of the form
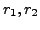 and
and 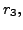 respectively. Let
respectively. Let
Secondly, a point ![]() is called an ORDINARY POINT for
(9.3.1) if
is called an ORDINARY POINT for
(9.3.1) if
![]() and
and ![]() admit power series expansion
(with non-zero radius of convergence) around
admit power series expansion
(with non-zero radius of convergence) around ![]()
![]() is called
a SINGULAR POINT for (9.3.1) if
is called
a SINGULAR POINT for (9.3.1) if ![]() is not an ordinary
point for (9.3.1).
is not an ordinary
point for (9.3.1).
The following are some examples for illustration of the utility of Theorem 9.3.1.
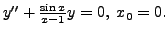
A K Lal 2007-09-12