Consider a linear second order equation of the type
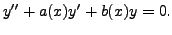 |
(9.2.1) |
Let 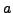 and
and 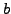 be analytic around the point
be analytic around the point 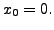 In such a case, we may hope to have a solution
In such a case, we may hope to have a solution 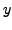 in terms
of a power series, say
in terms
of a power series, say
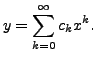 |
(9.2.2) |
In the absence of any
information, let us assume that (9.2.1) has a solution
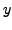 represented by (9.2.2). We substitute
(9.2.2) in Equation (9.2.1)
and try to find
the values of
represented by (9.2.2). We substitute
(9.2.2) in Equation (9.2.1)
and try to find
the values of 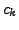 's. Let us take up an example for illustration.
's. Let us take up an example for illustration.
EXAMPLE 9.2.1
Consider the differential equation
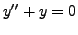 |
(9.2.3) |
Here
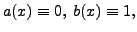 which are analytic around
which are analytic around 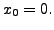
Solution: Let
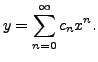 |
(9.2.4) |
Then
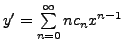 and
and
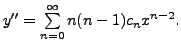 Substituting the
expression for
Substituting the
expression for
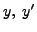 and
and
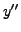 in Equation
(9.2.3), we get
in Equation
(9.2.3), we get
or, equivalently
Hence for all
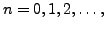
Therefore, we have
Here,  and
and 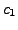 are
arbitrary. So,
are
arbitrary. So,
or
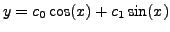 where
where  and
and 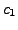 can be chosen
arbitrarily. For
can be chosen
arbitrarily. For 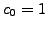 and
and 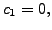 we get
we get
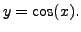 That is,
That is, 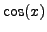 is a solution of the Equation
(9.2.3). Similarly,
is a solution of the Equation
(9.2.3). Similarly,
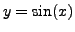 is also a solution
of Equation (9.2.3).
is also a solution
of Equation (9.2.3).
EXERCISE 9.2.2
Assuming that the solutions 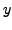 of the following differential equations
admit power series representation, find
of the following differential equations
admit power series representation, find 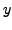 in terms of a power series.
in terms of a power series.
-
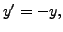 (centre at
(centre at 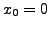 ).
).
-
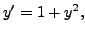 (centre at
(centre at 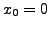 ).
).
- Find two linearly independent solutions of
-
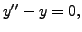 (centre at
(centre at 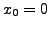 ).
).
-
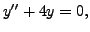 (centre at
(centre at 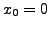 ).
).
A K Lal
2007-09-12
 In such a case, we may hope to have a solution
In such a case, we may hope to have a solution 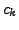 's. Let us take up an example for illustration.
's. Let us take up an example for illustration.
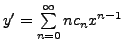 and
and
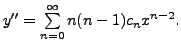 Substituting the
expression for
Substituting the
expression for
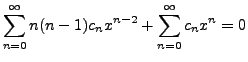
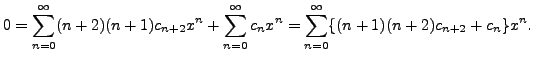

 and
and 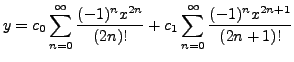
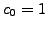 and
and 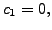 we get
we get