Next: Solutions in terms of Up: Introduction Previous: Introduction Contents
Now we quickly state some of the important properties of the power series. Consider two power series
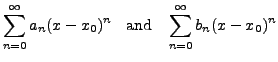
with radius of convergence
With
![]() and
and ![]() as defined above, we have the following properties
of the power series.
as defined above, we have the following properties
of the power series.
In particular, if
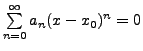 for all
for all
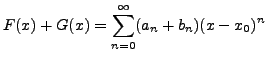
Essentially, it says that in the common part of the regions of convergence, the two power series can be added term by term.
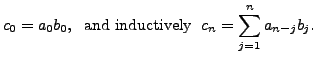
Then for all
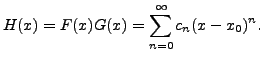
Note that for any 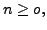 the coefficient of
the coefficient of 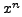 in
in
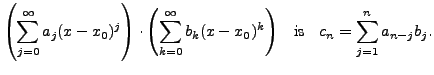
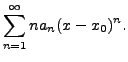
Note that it also has
![$\displaystyle \lim_{n \longrightarrow \infty} \sqrt[n]{\vert n a_n\vert} =
\li...
...im_{n \longrightarrow \infty} \sqrt[n]{\vert a_n\vert} = 1 \cdot \frac{1}{R_1}.$](img4342.png)
Let
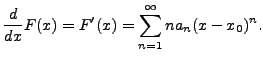
In other words, inside the region of convergence, the power series can be differentiated term by term.
In the following, we shall consider power series with ![]() as the centre.
Note that by a transformation of
as the centre.
Note that by a transformation of
![]() the centre of the power
series can be shifted to the origin.
the centre of the power
series can be shifted to the origin.
 defined by
defined by 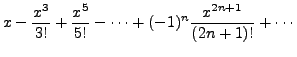 |
|||
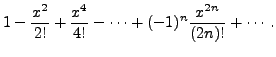 |
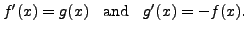
[Hint: Use Properties
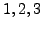 and
and 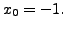
A K Lal 2007-09-12