Next: Properties of Power Series Up: Solutions Based on Power Previous: Solutions Based on Power Contents
In the previous chapter, we had a discussion on the methods of solving
where
In this chapter, we have a partial answer to the above question. In general, there are no methods of finding a solution of an equation of the form
where
In short,
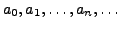 are called the coefficient
of the power series and
are called the coefficient
of the power series and ![]() is called the centre.
Note here that
is called the centre.
Note here that
![]() is the coefficient of
is the coefficient of
![]() and that the power series converges for
and that the power series converges for ![]() So, the set
So, the set
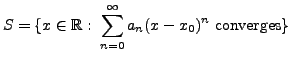
is a non-empty. It turns out that the set
Let ![]() be the radius of convergence of the power series
(9.1.1). Let
be the radius of convergence of the power series
(9.1.1). Let
![]() In the
interval
In the
interval ![]() the power series (9.1.1)
converges. Hence, it defines a real valued function and we denote
it by
the power series (9.1.1)
converges. Hence, it defines a real valued function and we denote
it by ![]() i.e.,
i.e.,
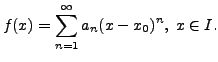
Such a function is well defined as long as
It is a natural question to ask how to find the radius of convergence of a power series (9.1.1). We state one such result below but we do not intend to give a proof.
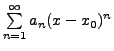 be a
power series with centre
be a
power series with centre
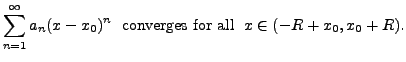
In this case, the power series
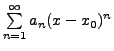 converges absolutely and
uniformly on
converges absolutely and
uniformly on
and diverges for all
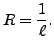
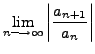 exists and
exists and
![$\displaystyle \lim_{n \longrightarrow \infty} \sqrt[n]{\vert a_n\vert} =
\lim_{n \longrightarrow \infty} \left\vert \frac{a_{n+1}}{a_n} \right\vert.$](img4283.png)
In case,
![]() does not tend to a limit as
does not tend to a limit as
![]() then the above theorem holds if we replace
then the above theorem holds if we replace
![]() by
by
![]()
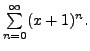 Here
Here 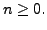 So,
So,
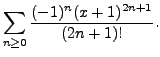 In this case, the centre
is
In this case, the centre
is
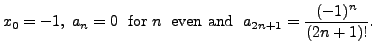
So,
Thus,
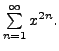 In this
case, we have
In this
case, we have
So,
![$\displaystyle \lim_{n\longrightarrow \infty}
\sqrt[2n+1]{\vert a_{2n+1}\vert} ...
...ox{ and }} \; \lim_{n\longrightarrow \infty}
\sqrt[2n]{\vert a_{2n}\vert} = 1.$](img4300.png)
Thus,
We let ![]() Then the power series
Then the power series
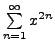 reduces to
reduces to
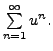 But then from
Example 9.1.6.1, we learned that
But then from
Example 9.1.6.1, we learned that
![]() converges for all
converges for all ![]() with
with ![]() Therefore, the original power series converges whenever
Therefore, the original power series converges whenever
![]() or
equivalently whenever
or
equivalently whenever ![]() So, the radius of convergence is
So, the radius of convergence is ![]() Note that
Note that
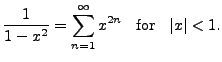
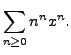 In this case,
In this case,
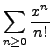 has coefficients
has coefficients
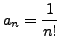 and it is
easily seen that
and it is
easily seen that
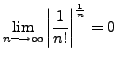 and the power series converges
for all
and the power series converges
for all
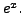
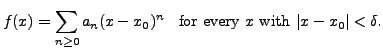
That is,