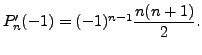Next: Laplace Transform Up: Legendre Equations and Legendre Previous: Introduction Contents
In many problems, the real number ![]() appearing in the Legendre
Equation (9.4.1), is a non-negative integer. Suppose
appearing in the Legendre
Equation (9.4.1), is a non-negative integer. Suppose
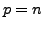 is a non-negative integer. Recall
is a non-negative integer. Recall
Case 1: Let
In either case, we have a polynomial solution for Equation (9.4.1).
Fix a positive integer ![]() and consider
and consider
![]() Then it can be checked that
Then it can be checked that
![]() if we choose
if we choose
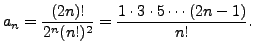
Using the recurrence relation, we have
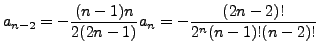
by the choice of
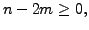 then
then
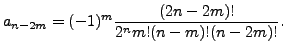
Hence,
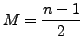 when
when
Similarly, if ![]() is a non-negative odd integer, then any
polynomial solution
is a non-negative odd integer, then any
polynomial solution ![]() of (9.4.1) which has only
odd powers of
of (9.4.1) which has only
odd powers of ![]() is a multiple of
is a multiple of ![]()
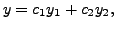
where
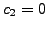 or
or
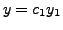 with
with
We have an alternate way of evaluating ![]() They are used
later for the orthogonality properties of the Legendre
polynomials,
They are used
later for the orthogonality properties of the Legendre
polynomials, ![]() 's.
's.
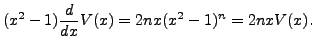
Now differentiating
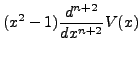 |
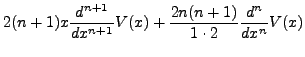 |
||
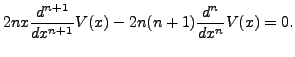 |
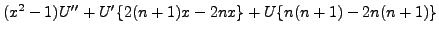 |
0 | ||
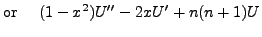 |

Also, let us note that
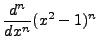 |
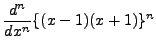 |
||
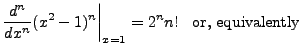
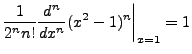
and thus
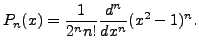
height6pt width 6pt depth 0pt
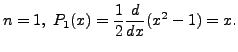
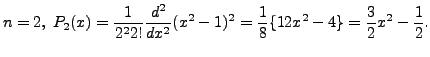
One may observe that the Rodrigu s formula
is very useful in the computation of
s formula
is very useful in the computation of ![]() for ``small"
values of
for ``small"
values of ![]()
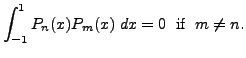 |
(9.4.8) |
Therefore,
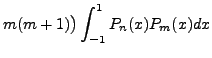 |
|||
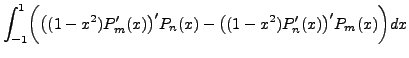 |
|||
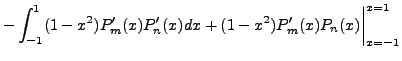 |
|||
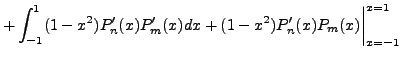 |
|||
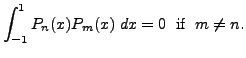
height6pt width 6pt depth 0pt
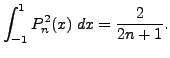 |
(9.4.11) |

Let us call
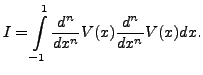 Note that for
Note that for
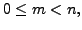
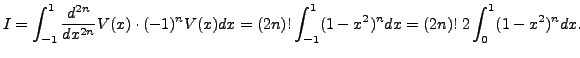
Now substitute
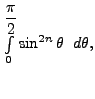 to get the required result.
height6pt width 6pt depth 0pt
to get the required result.
height6pt width 6pt depth 0pt
We now state an important expansion theorem. The proof is beyond the scope of this book.
![$\displaystyle f(x) = \sum_{n=0}^\infty a_n P_n(x), \;\; x \in [-1,
1]$](img4497.png)
where
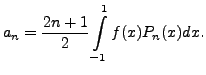
Legendre polynomials can also be generated by a suitable function. To do that, we state the following result without proof.
The function
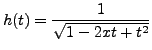 admits a power series expansion in
admits a power series expansion in ![]() (for small
(for small ![]() ) and
the coefficient of
) and
the coefficient of  in
in ![]() The function
The function ![]() is
called the GENERATING FUNCTION for the Legendre polynomials.
is
called the GENERATING FUNCTION for the Legendre polynomials.
Using the generating function (9.4.13), we can
establish the following relations:
The relations (9.4.14), (9.4.15) and
(9.4.16) are called recurrence relations for the Legendre
polynomials, ![]() The relation (9.4.14) is also
known as Bonnet's recurrence relation. We will now give the proof
of (9.4.14) using (9.4.13). The readers are
required to proof the other two recurrence relations.
The relation (9.4.14) is also
known as Bonnet's recurrence relation. We will now give the proof
of (9.4.14) using (9.4.13). The readers are
required to proof the other two recurrence relations.
Differentiating the generating function (9.4.13)
with respect to ![]() (keeping the variable
(keeping the variable ![]() fixed), we get
fixed), we get
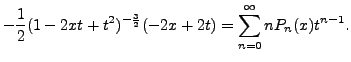
Or equivalently,
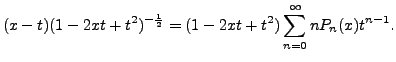
We now substitute
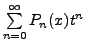 in the left hand
side for
in the left hand
side for
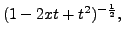 to get
to get
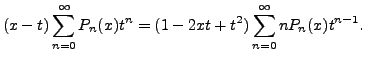
The two sides and power series in
This is clearly same as (9.4.14).
To prove (9.4.15), one needs to differentiate the
generating function with respect to ![]() (keeping
(keeping ![]() fixed) and
doing a similar simplification. Now, use the relations
(9.4.14) and (9.4.15) to get the relation
(9.4.16). These relations will be helpful in solving the
problems given below.
fixed) and
doing a similar simplification. Now, use the relations
(9.4.14) and (9.4.15) to get the relation
(9.4.16). These relations will be helpful in solving the
problems given below.
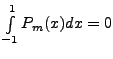 for all positive integers
for all positive integers 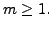
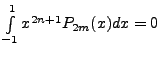 whenever
whenever 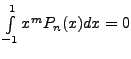 whenever
whenever 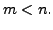
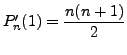 and
and