Orthogonal Trajectories

One among the many applications of differential equations is to find curves that intersect a given family of curves at right angles. In other words, given a family of curves, we wish to find curve (or curves) $\Gamma$ which intersect orthogonally with any member of (whenever they intersect). It is important to note that we are not insisting that $\Gamma$ should intersect every member of but if they intersect, the angle between their tangents, at every point of intersection, is $90^\circ.$ Such a family of curves $\Gamma$ is called ``orthogonal trajectories" of the family That is, at the common point of intersection, the tangents are orthogonal. In case, the family and are identical, we say that the family is self-orthogonal.

Before procedding to an example, let us note that at the common point of intersection, the product of the slopes of the tangent is 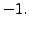$ -1.$ In order to find the orthogonal trajectories of a family of curves parametrized by a constant we eliminate between and $y^\prime.$ This gives the slope at any point and is independent of the choice of the curve. Below, we illustrate, how to obtain the orthogonal trajectories.

EXAMPLE 7.6.11 Compute the orthogonal trajectories of the family of curves given by

$\displaystyle F : \hspace{.2in} y^2 = c x^3,$

(7.6.7)

where is an arbitrary constant.

Solution: Differentiating (7.6.7), we get

$\displaystyle 2 y y^\prime = 3 c x^2.$

(7.6.8)

Elimination of

between (7.6.7) and (7.6.8), leads to

$\displaystyle y^\prime = \frac{ 3 c x^2}{2 y} = \frac{3}{2x} \cdot \frac{ c x^3}{y} = \frac{3y}{2x}.$

(7.6.9)

At the point

if any curve intersects orthogonally, then (if its slope is $y^\prime$ ) we must have

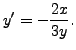
$\displaystyle y^\prime = - \frac{2x}{3y}.$

Solving this differential equation, we get

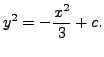
$\displaystyle y^2 = - \frac{x^2}{3} + c.$

Or equivalently, 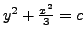$y^2 + \frac{x^2}{3} = c$ is a family of curves which intersects the given family

orthogonally.

Below, we summarize how to determine the orthogonal trajectories.
Step 1: Given the family determine the differential equation,

$\displaystyle y^\prime = f(x,y),$

(7.6.10)

for which the given family

are a general solution. The Equation (7.6.10) is obtained by the elimination of the constant

appearing in

``using the equation obtained by differentiating this equation with respect to

".
Step 2: The differential equation for the orthogonal trajectories is then given by

$\displaystyle y^\prime = - \frac{1}{f(x,y)}.$

(7.6.11)

Final Step: The general solution of (7.6.11) is the orthogonal trajectories of the given family.

In the following, let us go through the steps.

EXAMPLE 7.6.12 Find the orthogonal trajectories of the family of stright lines

$\displaystyle y = m x + 1,$

(7.6.12)

where is a real parameter.

Solution: Differentiating (7.6.12), we get $y^\prime = m.$ So, substituting

in (7.6.12), we have $y = y^\prime x + 1.$ Or equivalently,

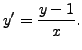
$\displaystyle y^\prime = \frac{y-1}{x}.$

So, by the final step, the orthogonal trajectories satisfy the differential equation

$\displaystyle y^\prime = \frac{x}{1-y}.$

(7.6.13)

It can be easily verified that the general solution of (7.6.13) is

$\displaystyle x^2 + y^2 - 2 y = c,$

(7.6.14)

where

is an arbitrary constant. In other words, the orthogonal trajectories of the family of straight lines (7.6.12) is the family of circles given by (7.6.14).

EXERCISE 7.6.13

Find the orthogonal trajectories of the following family of curves (the constant appearing below is an arbitrary constant).
Show that the one parameter family of curves $y^2 = 4 k (k+x), \; k \in {\mathbb{R}}$ are self orthogonal.
Find the orthogonal trajectories of the family of circles passing through the points and

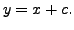
A K Lal 2007-09-12