Next: Orthogonal Trajectories Up: Differential Equations Previous: Miscellaneous Remarks Contents
As we had seen, there are no methods to solve a general equation of the form
The answers to the above two questions are not simple. But there
are partial answers if some additional restrictions
on the function ![]() are imposed.
The details are discussed in this
section.
are imposed.
The details are discussed in this
section.
For
![]() with
with
![]() we define
we define
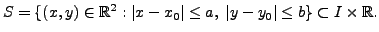
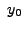 is called the INITIAL VALUE.
is called the INITIAL VALUE.
Further, we assume that ![]() and
and ![]() are
finite. Let
are
finite. Let
Such an
In the absence of any knowledge of a solution of IVP
(7.6.2), we now try to find an approximate solution. Any
solution of the IVP (7.6.2) must satisfy the initial
condition
![]() Hence, as a crude approximation to the
solution of IVP (7.6.2), we define
Hence, as a crude approximation to the
solution of IVP (7.6.2), we define
Now the Equation (7.6.3) appearing in Proposition 7.6.2, helps us to refine or improve the approximate solution
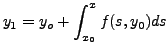
and for
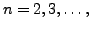 we inductively define
we inductively define
![$\displaystyle y_n = y_0 + \int_{x_0}^x f(s, y_{n-1}(s)) ds
{\mbox{ for all }} \; x \in [x_0 - h, x_0 + h].$](img3601.png)
As yet we have not checked a few things, like whether the point
![]() or not. We formalise the theory in the latter part of this
section. To get ourselves motivated, let us apply the above method to the
following IVP.
or not. We formalise the theory in the latter part of this
section. To get ourselves motivated, let us apply the above method to the
following IVP.
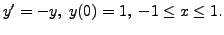
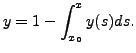
We have
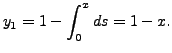
So,
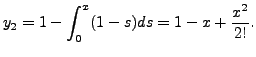
By induction, one can easily verify that
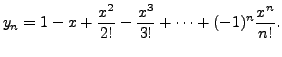
Note: The solution of the given IVP is
This example justifies the use of the word approximate solution for the
We now formalise the above procedure.
Then
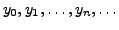 are
called Picard's successive approximations to the IVP (7.6.2).
are
called Picard's successive approximations to the IVP (7.6.2).
Whether (7.6.4) is well defined or not is settled in the following proposition.
So,
The rest of the proof is by the method of induction. We have established
the result for ![]() namely
namely
Assume that for
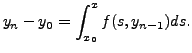
But then by induction hypotheses
This shows that
Let us again come back to Example 7.6.3 in the light of Proposition 7.6.2.
By Proposition 7.6.2, on this set
Therefore, the approximate solutions
![$ [-\displaystyle\frac{1}{2}, \displaystyle\frac{1}{2} ],$](img3646.png) if we use Proposition 7.6.2.
if we use Proposition 7.6.2.
Observe that the exact solution
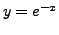 and the approximate
solutions
and the approximate
solutions ![]() 's of Example 7.6.3 exist on
's of Example 7.6.3 exist on ![]() But the approximate solutions as seen above are defined in the interval
But the approximate solutions as seen above are defined in the interval
![$ [-\displaystyle\frac{1}{2}, \displaystyle\frac{1}{2} ].$](img3648.png)
That is, for any IVP, the approximate solutions ![]() 's may exist on a
larger interval as compared
to the interval obtained by the application of the
Proposition 7.6.2.
's may exist on a
larger interval as compared
to the interval obtained by the application of the
Proposition 7.6.2.
We now consider another example.
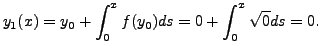
A similar argument implies that
 and
and
Also
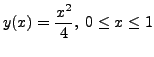 is a
solution of (7.6.6) and the
is a
solution of (7.6.6) and the ![]() 's do not
converge to
's do not
converge to
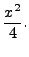 Note here that the IVP
(7.6.6) has at least two solutions.
Note here that the IVP
(7.6.6) has at least two solutions.
The following result is about the existence of a unique solution to a class of IVPs. We state the theorem without proof.
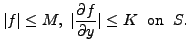
Let
Whenever we talk of the Picard's theorem, we mean it in this local sense.
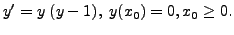
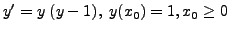
is
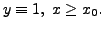
has solutions
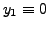 as well as
as well as
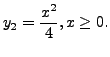 Why does the
existence of the two solutions not contradict the
Picard's theorem?
Why does the
existence of the two solutions not contradict the
Picard's theorem?
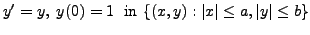
for any