Next: Initial Value Problems Up: Differential Equations Previous: Linear Equations Contents
In Section 7.4, we have
learned to solve the linear equations. There are many other equations,
though not linear, which are also amicable for solving.
Below, we consider a few classes of equations which can be solved. In this
section or in the sequel, ![]() denotes
denotes
![]() or
or
![]() A word of caution is needed here. The method described below are
more or less ad hoc methods.
A word of caution is needed here. The method described below are
more or less ad hoc methods.
Solve
![]()
Solution: Differentiating
with respect to ![]() and replacing
and replacing
![]() by
by ![]() we get
we get
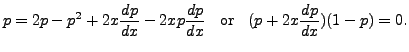
So, either
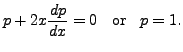
That is, either
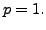 Eliminating
Eliminating
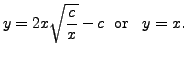
The first solution is a one-parameter family of solutions, giving us a general solution. The latter one is a solution but not a general solution since it is not a one parameter family of solutions.
Solve
![]() where
where ![]() is a constant.
is a constant.
Solution: We
equivalently rewrite the given equation, by (arbitrarily)
introducing a new parameter ![]() by
by
from which it follows
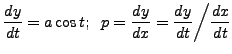
and so
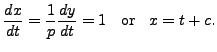
Therefore, a general solution is
Find the general solution of
![]()
Solution: Recall that
![]() Now, from the given equation, we have
Now, from the given equation, we have
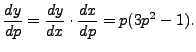
Therefore,
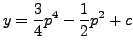
(regarding
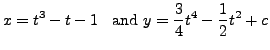
where
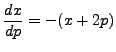 ( a linear equation in
( a linear equation in
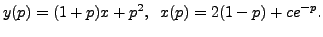
A K Lal 2007-09-12