Separable Equations

In general, it may not be possible to find solutions of $y^\prime = f(x,y)$ , where $f$ is an arbitrary continuous function. But there are special cases of the function $f$ for which the above equation can be solved. One such set of equations is

$$\index{Separable Equations} y^\prime = g (y) h(x).$$ (7.2.1)

The Equation (7.2.1) is called a SEPARABLE EQUATION and is equivalent to

$$\frac{1}{g(y)} \frac{dy}{dx} = h(x).$$

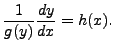
Integrating with respect to $x,$ we get

$$H(x) = \int h(x) dx = \int \frac{1}{g(y)} \frac{dy}{dx} dy = \int \frac{dy}{g(y)} = G(y) + c,$$

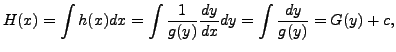
where $c$ is a constant. Hence, its implicit solution is

$$G(y) + c = H(x).$$

EXAMPLE 7.2.1  

1. Solve: $y^\prime = y (y-1).$
   Solution: Here, $g(y) = y \; (y-1)$ and $h(x) = 1.$ Then
   $$\int \frac{dy}{y \; (y-1)} = \int dx.$$
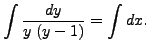
   By using partial fractions and integrating, we get
   $$y = \frac{1}{1 - e^{x+c}}\;,$$
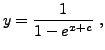
   where $c$ is a constant of integration.
2. Solve $y^\prime = y^2.$
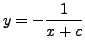   Solution: It is easy to deduce that $y = -\displaystyle\frac{1}{x+c}$ , where $c$ is a constant; is the required solution.

   Observe that the solution is defined, only if $x + c \neq 0$ for any $x.$ For example, if we let $y(0) = a,$ then $y = -\displaystyle\frac{a}{ax - 1}$ exists as long as $a x - 1 \neq 0.$