Next: Exact Equations Up: Separable Equations Previous: Separable Equations Contents
There are many equations which are not of the form 7.2.1, but by a suitable substitution, they can be reduced to the separable form. One such class of equation is
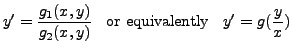
where
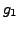 and
and 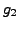 are homogeneous functions of the same degree in
are homogeneous functions of the same degree in
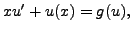
which is a separable equation in
Letting
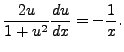
On integration, we get
or
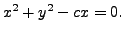
The general solution can be re-written in the form
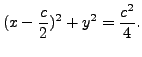
This represents a family of circles with center
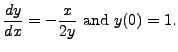
Notice that it is a separable equation and it is easy to verify that
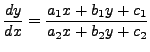
can also be solved by the above method by replacing
This condition changes the given differential equation into
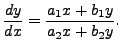 Thus, if
Thus, if
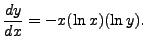
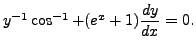
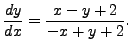
A K Lal 2007-09-12