Next: Separable Equations Up: Differential Equations Previous: Differential Equations Contents
There are many
branches of science and engineering where differential equations
arise naturally. Now a days, it finds applications in many areas including
medicine, economics and social sciences. In this context,
the study of differential equations assumes importance. In
addition, in the study of
differential equations, we also see the applications of many
tools from analysis and linear algebra. Without spending more
time on motivation,
(which will be clear as we go along) let us start with the following
notations.
Let ![]() be an independent variable and let
be an independent variable and let ![]() be a dependent variable
of
be a dependent variable
of ![]() . The derivatives of
. The derivatives of ![]() (with respect
to
(with respect
to ![]() ) are denoted by
) are denoted by
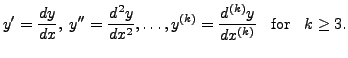
The independent variable will be defined for an interval
A differential equation is a relationship between the independent variable and the unknown dependent function along with its derivatives. More precisely, we have the following definition.
Some examples of differential equations are
In Example 7.1, the order of Equations 1, 3, 4, 5 are one, that of Equations 2, 6 and 8 are two and the Equation 7 has order three.
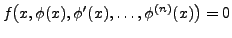 for all
for all
If ![]() is a solution of an ODE (7.1.1) on
is a solution of an ODE (7.1.1) on ![]() , we also say that
, we also say that
![]() satisfies (7.1.1). Sometimes a solution
satisfies (7.1.1). Sometimes a solution ![]() is also called an INTEGRAL.
is also called an INTEGRAL.
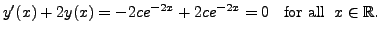
Hence,
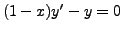
on any interval that does not contain the point
is called a one parameter family of functions and
| (7.1.5) |
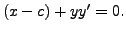
Now, eliminating
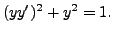
In Example 7.1.10.1, we see that ![]() is not
defined explicitly as a function of
is not
defined explicitly as a function of ![]() but implicitly defined by
(7.1.3). On the other hand
but implicitly defined by
(7.1.3). On the other hand
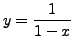 is an explicit solution in Example
7.1.5.2.
is an explicit solution in Example
7.1.5.2.
Let us now look at some geometrical interpretations of the
differential Equation (7.1.2). The Equation
(7.1.2) is a relation between 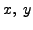 and the slope
of the function
and the slope
of the function ![]() at the point
at the point ![]() For instance, let us find
the equation of the curve passing through
For instance, let us find
the equation of the curve passing through
![]() and whose slope at each point
and whose slope at each point
![]() is
is
![]() If
If ![]() is the
required curve, then
is the
required curve, then ![]() satisfies
satisfies
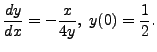
It is easy to verify that
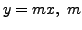 real (family of lines).
real (family of lines).
A K Lal 2007-09-12