Next: Error Estimates and Convergence Up: Introduction Previous: Introduction Contents
For a small step size ![]() , the derivative
, the derivative
![]() is close enough to the ratio
is close enough to the ratio
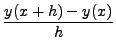 . In the Euler's method, such an approximation
is attempted. To recall, we consider the problem (
. In the Euler's method, such an approximation
is attempted. To recall, we consider the problem (![[*]](crossref.png) ).
Let
).
Let
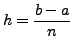 be the step size and
let
be the step size and
let
![]() with
with ![]() . Let
. Let ![]() be the approximate value of
be the approximate value of
![]() at
at
![]() . We define
. We define
![[*]](crossref.png) ) is called the EULER'S METHOD.
For convenience, the value
) is called the EULER'S METHOD.
For convenience, the value
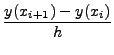 if
if ![[*]](crossref.png) ), we have
), we have
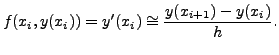
![[*]](crossref.png) ) from the following point of view. The integration of (
) from the following point of view. The integration of (![[*]](crossref.png) ) yields
) yields
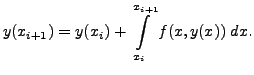
The integral on the right hand side is approximated, for sufficiently small value of
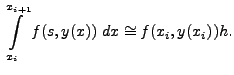
![[*]](crossref.png) ) by considering the Taylor's expansion
) by considering the Taylor's expansion
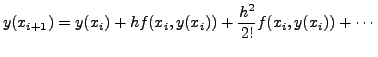
and neglecting terms that contain powers of
We illustrate the Euler's method with an example. The example is only for illustration. In
(![[*]](crossref.png) ), we do not need numerical computation at each step as we know the exact
value of the solution. The purpose of the example is to have a feeling for the behaviour of
the error and its estimate. It will be more transparent to look at the percentage of error.
It may throw more light on the propagation of error.
), we do not need numerical computation at each step as we know the exact
value of the solution. The purpose of the example is to have a feeling for the behaviour of
the error and its estimate. It will be more transparent to look at the percentage of error.
It may throw more light on the propagation of error.
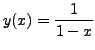 . Calculate the error
at each step and tabulate the results.
. Calculate the error
at each step and tabulate the results.
![[*]](crossref.png) ), we note that
), we note that
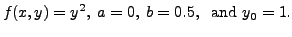
The Euler's algorithm now reads as
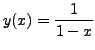 is a solution
of the given IVP.
So, the absolute value of the error at the
is a solution
of the given IVP.
So, the absolute value of the error at the
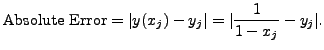
See the Tables
![[*]](crossref.png) and
and ![[*]](crossref.png) for the calculation of errors (up to
for the calculation of errors (up to
We now give a sample flow chart for the Euler's method.
A K Lal 2007-09-12