Next: Gauss's and Stirling's Formulas Up: Lagrange's Interpolation Formula Previous: Divided Differences Contents
![$\displaystyle \delta[x_0,x_1] = \frac{f(x_1) - f(x_0)}{x_1 - x_0} =
\frac{f(x_0)}{x_0 - x_1} + \frac{f(x_1)}{x_1 - x_0}.$](img5247.png)
Let us assume that the result is true for
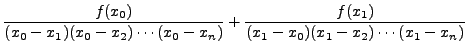 |
|||
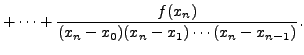 |
![$\displaystyle \frac{
\delta[x_1,x_2, \ldots,x_{n+1}] -
\delta[x_0,x_1,\ldots,x_n]}{x_{n+1} - x_0}$](img5253.png) |
|||
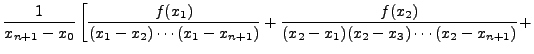 |
|||
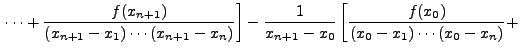 |
|||
![$\displaystyle \left.
\frac{f(x_1)}{(x_1-x_0)(x_1-x_2)\cdots(x_1 - x_{n})} + \cdots +
\frac{f(x_{n})}{(x_{n}-x_0)\cdots(x_{n} - x_{n-1})} \right]$](img5256.png) |
Now, if a function is approximated by a polynomial of degree ![]() then , its
then , its
![]() divided difference relative to
divided difference relative to
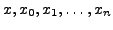 will be zero,(Remark 12.2.6)
i.e.,
will be zero,(Remark 12.2.6)
i.e.,
Using this result, Theorem 12.3.1 gives
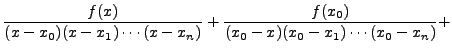 |
|||
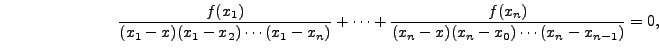 |
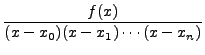 |
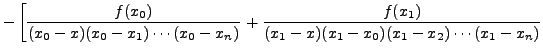 |
||
![$\displaystyle \hspace{.5in} \left. + \cdots +
\frac{f(x_{n})}{(x_{n}-x)(x_{n}-x_0)\cdots(x_{n} -
x_{n-1})}\right],$](img5263.png) |
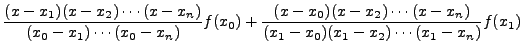 |
|||
 |
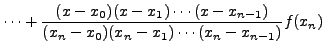 |
||
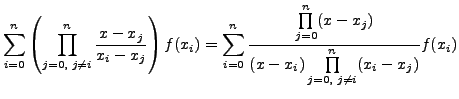 |
|||
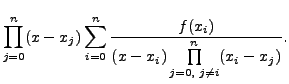 |
Note that the expression on the right is a polynomial of degree
![]() and takes the value
and takes the value ![]() at
at ![]() for
for
![]()
This polynomial approximation is called LAGRANGE'S INTERPOLATION FORMULA.
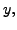 i.e. while using
the table of values, we take tabular points as
i.e. while using
the table of values, we take tabular points as
|
|
0 | 1 | 2 | 3 | 4 |
| |
9.3 | 9.6 | 10.2 | 10.4 | 10.8 |
|
|
11.40 | 12.80 | 14.70 | 17.00 | 19.80 |
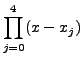 |
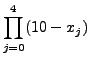 |
||
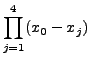 |
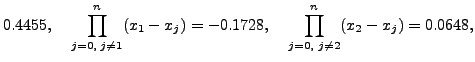 |
||
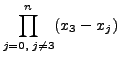 |
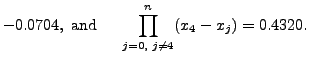 |
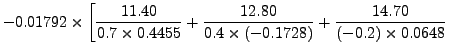 |
|||
![$\displaystyle \hspace{.15in} \left. + \frac{17.00}{(-0.4)\times (-0.0704)} +
\frac{19.80}{(-0.8) \times 0.4320} \right]$](img5283.png) |
|||
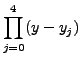 |
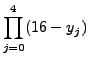 |
||
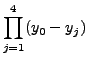 |
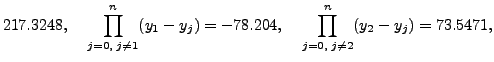 |
||
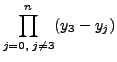 |
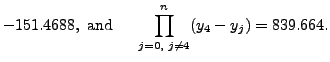 |
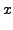 |
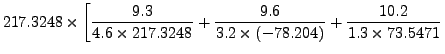 |
||
![$\displaystyle \hspace{.15in}
\left. + \frac{10.40}{(-1.0)\times (-151.4688)} +
\frac{10.80}{(-3.8) \times839.664} \right]$](img5295.png) |
|||
|
|
360 | 365 | 373 | 383 | 390 |
| |
154.0 | 165.0 | 190.0 | 210.0 | 240.0 |
|
|
5.60 | 5.90 | 6.50 | 6.90 | 7.20 |
| |
2.30 | 1.80 | 1.35 | 1.95 | 2.00 |
A K Lal 2007-09-12