Next: Lagrange's Interpolation formula Up: Lagrange's Interpolation Formula Previous: Introduction Contents
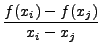
for any two points
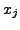 is called the FIRST DIVIDED DIFFERENCE of
is called the FIRST DIVIDED DIFFERENCE of
Let us assume that the function
![]() is linear. Then
is linear. Then
![]() is constant for any two tabular points
is constant for any two tabular points ![]() and
and 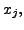 i.e., it is independent of
i.e., it is independent of ![]() and
and ![]() Hence,
Hence,
![$\displaystyle \delta[x_i, x_j] = \frac{f(x_i) - f(x_j)}{x_i - x_j}= \delta[x_j,x_i].$](img5171.png)
Thus, for a linear function ![]() if we take the points
if we take the points 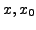 and
and ![]() then,
then,
![]() i.e.,
i.e.,
![$\displaystyle \frac{f(x) - f(x_0)}{x - x_0}= \delta[x_0,x_1].$](img5174.png)
Thus,
So, if ![]() is approximated with a linear polynomial, then the value of
the function at any point
is approximated with a linear polynomial, then the value of
the function at any point ![]() can be calculated by using
can be calculated by using
![]() where
where
![]() is the first divided difference of
is the first divided difference of ![]() relative
to
relative
to ![]() and
and ![]()
![$\displaystyle \delta[x_i, x_j,x_k] = \frac{\delta[x_j,x_k] - \delta[x_i,x_j]}{x_k -
x_i}$](img5179.png)
is defined as SECOND DIVIDED DIFFERENCE of
If ![]() is a second degree polynomial then
is a second degree polynomial then
![]() is a linear function
of
is a linear function
of ![]() Hence,
Hence,
![$\displaystyle \delta[x_i, x_j,x_k] = \frac{\delta[x_j,x_k] - \delta[x_i,x_j]}{x_k -
x_i} \;\;{\mbox{ is constant}}.$](img5183.png)
In view of the above, for a polynomial function of degree 2, we have
![]() Thus,
Thus,
![$\displaystyle \frac{\delta[x,x_0] - \delta[x_0,x_1]}{x - x_1} =
\delta[x_0,x_1,x_2].$](img5185.png)
This gives,
From this we obtain,
So, whenever ![]() is approximated with a second degree polynomial, the
value of
is approximated with a second degree polynomial, the
value of ![]() at any point
at any point ![]() can be computed using the above polynomial,
which uses the values at three points
can be computed using the above polynomial,
which uses the values at three points 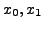 and
and ![]()
| |
0 | 1 | 2 |
|
|
0.1 | 0.16 | 0.2 |
| |
1.12 | 1.24 | 1.40 |
![$\displaystyle \frac{\delta[x_1,x_2] -
\delta[x_0,x_1]}{x_2 - x_0} = (4-2)/(0.2-0.1) = 20.$](img5197.png) |
Therefore
| 322.8 | 324.2 | 325 | |
| 2.50893 | 2.51081 | 2.5118 |
![$\displaystyle \delta[x_0,x_1,x_2] =
\frac{f(x_0)}{(x_0-x_1)(x_0-x_2)} +
\frac{f(x_1)}{(x_1-x_0)(x_1-x_2)}+\frac{f(x_2)}{(x_2-x_0)(x_2-x_1)}.$](img5202.png)
So,
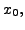
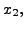
![$ \;\delta[x_0,x_1,x_2] =
\displaystyle\frac{\Delta^2 y_0}{2
h^2}=\displaystyle\frac{\nabla^2 y_2}{2 h^2},$](img5206.png) where
where
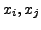 and
and 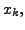 is always zero.
is always zero.
Now, we define the
![]() divided difference.
divided difference.
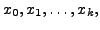 is defined recursively as
is defined recursively as
![$\displaystyle \delta[x_0,x_1,\ldots,x_k] = \frac{\delta[x_1,x_2,\ldots,x_k] -
\delta[x_0,x_1, \ldots,x_{k-1}]}{x_k - x_0}.$](img5212.png)
It can be shown by mathematical induction that for equidistant points,
In general,
![$\displaystyle \delta[x_i,x_{i+1}, \ldots, x_{i+n}] =
\frac{\Delta^n y_i}{n! h^n},$](img5216.png)
where
Solution:By definition, we have
![$\displaystyle \delta[x,x_0,x_1]=\frac{\delta[x,x_0]-\delta[x_0,x_1]}{(x-x_1)},$](img5221.png)
so,
![$\displaystyle \delta[x,x_0]=\frac{f(x)-f(x_0)}{(x-x_0)},$](img5223.png)
we get the desired result.
where,
Further show that
![]() for
for ![]()
Here,
![]() is called the remainder term.
is called the remainder term.
It may be observed here that the expression ![]() is a
polynomial of degree
is a
polynomial of degree ![]() and
and
![]() for
for
![]()
Further, if ![]() is a polynomial of degree
is a polynomial of degree ![]() then in view of
the Remark 12.2.6, the remainder term,
then in view of
the Remark 12.2.6, the remainder term,
![]() as it is a multiple of the
as it is a multiple of the
![]() divided difference, which is 0
.
divided difference, which is 0
.