Next: Central Difference Operator Up: Difference Operator Previous: Forward Difference Operator Contents
In particular, for ![]() we get
we get
Note that
Solution: We have
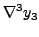 |
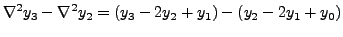 |
||
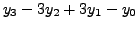 |
|||
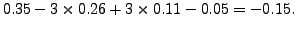 |
![$\displaystyle f(x)-f(x-h)=\left[x^2 + ax +b
\right]- \left[ (x-h)^2+a(x-h)+b \right]$](img4950.png) |
|||
![$\displaystyle \nabla f(x)-\Delta f(x-h)
= [2xh-h^2 + ah]-[2(x-h)h- h^2+ ah] = 2 h^2,$](img4953.png) |
|||
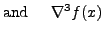 |
|
|
|
||||
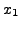
|
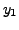
|
|
|||
|
|
|
|
|
||
| &vellip#vdots; | |||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 | 10 | 11 | 12 | 13 | 14 |
|
|
5.0 | 5.4 | 6.0 | 6.8 | 7.5 | 8.7 |
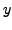
|
|
|
|
|
||
| 9 | 5 | 0.4 = 5.4 - 5 | 0.2 = 0.6 - 0.4 | 0= 0.2-0.2 | -.3 = -0.3 - 0.0 | 0.6 = 0.3 - (-0.3) |
| 10 | 5.4 | 0.6 | 0.2 | -0.3 | 0.3 | |
| 11 | 6.0 | 0.8 | -0.1 | 0.0 | ||
| 12 | 6.8 | 0.7 | -0.1 | |||
| 13 | 7.5 | 0.6 | ||||
| 14 | 8.1 |
In the similar manner, the backward difference table is written as follows:
|
|
|
|
|
|||
| 9 | 5 | |||||
| 10 | 5.4 | 0.4 | ||||
| 11 | 6 | 0.6 | 0.2 | |||
| 12 | 6.8 | 0.8 | 0.2 | 0.0 | ||
| 13 | 7.5 | 0.7 | -0.1 | - 0.3 | -0.3 | |
| 14 | 8.1 | 0.6 | -0.1 | 0.0 | 0.3 | 0.6 |
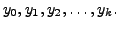 Hence show that
Hence show that
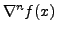 is constant and
is constant and
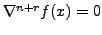 for
for
A K Lal 2007-09-12