Next: Backward Difference Operator Up: Difference Operator Previous: Difference Operator Contents
We define the FORWARD DIFFERENCE OPERATOR, denoted by ![]() as
as
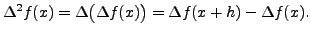
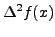 |
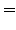 |
||
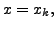 we get,
we get,
and
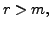
Solution: Here,
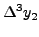 |
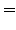 |
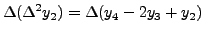 |
|
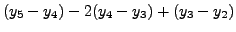 |
|||
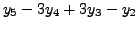 |
|||
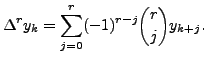
Thus the
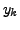 uses the values at
uses the values at
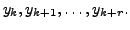
![$\displaystyle f(x+h)-f(x)=\left[(x+h)^2 + a(x+h) +b
\right]- \left[ x^2+ax+b \right]$](img4897.png) |
|||
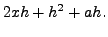 |
![$\displaystyle \Delta f(x+h)-\Delta f(x)
= [2(x+h)h+h^2 + ah]-[2xh+h^2+ah]=2 h^2,$](img4899.png) |
|||
 |
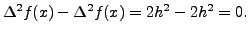 |
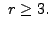
The reader is advised to prove the above statement.
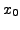
|
|
|
|
|
|
|
|
|
|
|
||
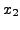
|
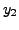
|
|
|
||
| &vellip#vdots; | |||||
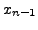
|
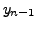
|
|
|||
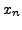
|
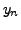
|
|
|
|
|||||||
|
|
||||||||
|
|
|
|
||||||
|
|
|
|||||||
|
|
|
|
||||||
| &vellip#vdots; |
|
|||||||
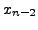
|
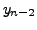
|
|
||||||
|
|
|
|||||||
|
|
|
|
||||||
|
|
||||||||
|
|
|
However, in the following, we shall mostly adhere to horizontal form only.
A K Lal 2007-09-12