DEFINITION 11.2.19 (Central Difference Operator)
The FIRST CENTRAL DIFFERENCE OPERATOR, denoted by 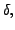 is defined by
is defined by
and the #MATH5164#
MATHEND000# CENTRAL DIFFERENCE OPERATOR is defined as
Thus,
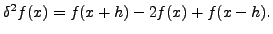
In particular, for 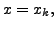 define
define
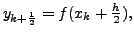 and
and
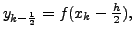 then
then
Thus, 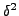 uses the table
of
uses the table
of
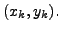 It is easy to see that only the even central differences use the tabular
point values
It is easy to see that only the even central differences use the tabular
point values
A K Lal
2007-09-12
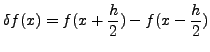
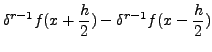
![]() define
define
![]() and
and
![]() then
then