Transformation of moments and products of area
from one system to another rotated with respect to
the first one: We just learnt that if we
translate an area so that its centriod moves to another
point, how its second moments of inertia and products
of inertia change when the axes passing through the
centroid and the other set of axes are parallel.
We now study how the moments and products are related
when we calculate them about another set of axes
that an rotated with respect to the first one. So
we consider a set of area (xy) and another on (x'y')
rotated with respect to the first one by an angle θ
(see figure 1).
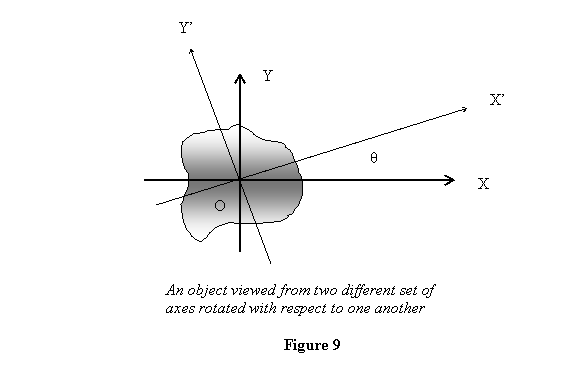
We wish to relate 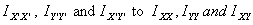 .
In lecture 1, we have already learnt that .
In lecture 1, we have already learnt that
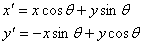
This gives
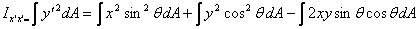
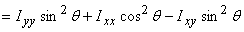
changing 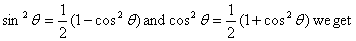
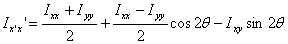

Similarly
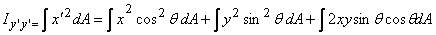
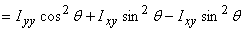
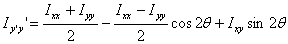
and
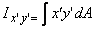
= 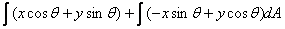
= 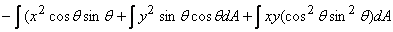
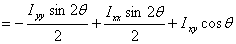
Thus
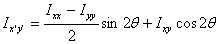
This gives the second moment and product about a set of
axis (x'y') rotated about the other set (xy). Let us
now discuss some examples.
As expected for a circular area, no matter about which
set of axes you calculate 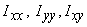 ,
it will always come out to be the same because the area
looks the sum from all set axes. What is interesting,
however, is that for a square also the moments and product
of area are the same with respect to any set of axes
passing through its centre. It happens because with respect
to its centre, the IXX and IYY for
a square are the same i.e. ,
it will always come out to be the same because the area
looks the sum from all set axes. What is interesting,
however, is that for a square also the moments and product
of area are the same with respect to any set of axes
passing through its centre. It happens because with respect
to its centre, the IXX and IYY for
a square are the same i.e. 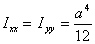 and and 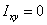 .
This is left as an exercise for you to show. .
This is left as an exercise for you to show.
We now use for formulae derived above to obtain what we
call the principal set of axes for a plane area.
The principal set of axes at a point are those for which
the product of inertia vanishes i.e. about the principal
set of axes 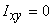 .
Let us see how we determine these axes if we know .
Let us see how we determine these axes if we know  about
a given set of axes. In the following we refer to the
principal set of axes as (1,2) where 1 refers
to the x-axis and 2 to the y-axis. We know
that we want about
a given set of axes. In the following we refer to the
principal set of axes as (1,2) where 1 refers
to the x-axis and 2 to the y-axis. We know
that we want
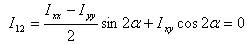
where α is the angle the principal set of axes make
with the (xy) set of axes. The equation above gives
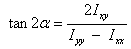
The principal set of axes has one more property: The moments
of area is maximum one of the principal axis (say x-axis)
and minimum about the other (y-axis). This is seen as
follow: Since
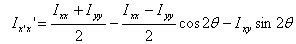
Let us find θ for which IX'X' is
a maximum or a minimum. The condition
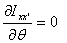
gives
 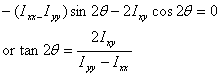
This is the same angle a that makes IXY vanish.
This means
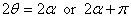
Thus
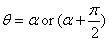
When α makes the function IXX a
maximum, the angle 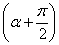 makes IYY a
minimum. I'll leave it for you to show that. Thus the
principal set of axes are also those about which the
II nd moment of area is maximum about one axis and minimum
about the other. Notice that for a square, any set of
axes passing through its centre is a principal set of
axes. This follows from the exercise that you did above.
As a related quantity, we also define polar
moment of an area . This is calculated as makes IYY a
minimum. I'll leave it for you to show that. Thus the
principal set of axes are also those about which the
II nd moment of area is maximum about one axis and minimum
about the other. Notice that for a square, any set of
axes passing through its centre is a principal set of
axes. This follows from the exercise that you did above.
As a related quantity, we also define polar
moment of an area . This is calculated as
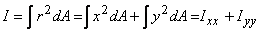
Since r2 is
independence of the (xy) system chosen, I is
the same about any set of axes passing through a point.
Having defined these concepts, at the end I will point
out that in a similar manner IInd moment of mass can
also be defined. We will elaborate on that more in the
later lectures on dynamics when we deal with the rotation
of rigid bodies.
Lecture 8 and 9 conclude our introduction to the properties
of surfaces.
|