Transfer theorem: Let the centroid of an area be at point ( x₀ y₀ ) with respect to the set of axes (xy). Let ( x' y' ) be a parallel set of axes passing through the centroid. Then

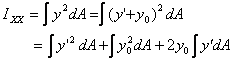
But by definition

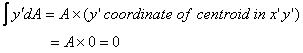
which gives

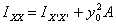
This is how the moment of area of a plane about an axis is related to the moment of the same area about another axis parallel to the previous one but passing through the centroid. Similarly it is easily shown that

.

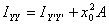and

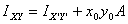
We now solve an example to show the application of this theorem.

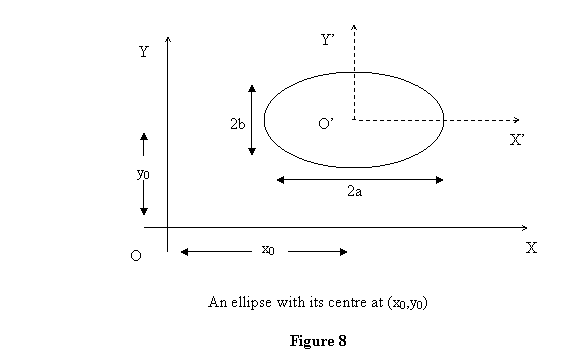
Example 3 : Calculate the second moments and products of area of an ellipse with its centre at (x₀ ,y₀ )

In a previous exercise, you have already calculated the second moments and products of area of an ellipse about its centre, which is also its centroid. These are:

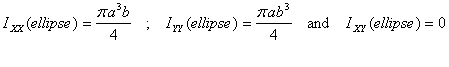
We use these results now in applying the transfer theorem to obtain moments and products of area of the ellipse about a different origin (see figure 8) . Thus

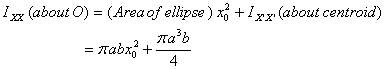
Similarly
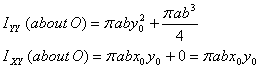