Let us now solve a few examples.
Example1: Let us start with a simple
example of a square of side a with its center of the
origin (see figure 2).
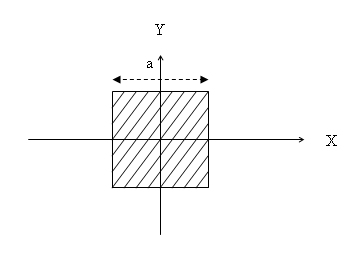
Figure 3
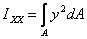
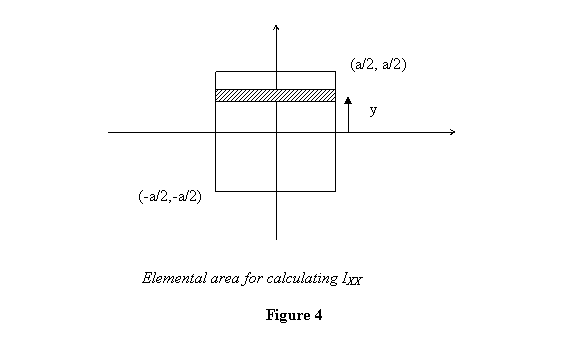
To calculate this, we choose the elemental area as shown
in figure 4 and integrate. Then
dA = ady
so that
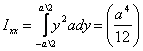
Similarly for calculating IYY we
choose a vertical elemental area and calculate
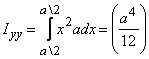
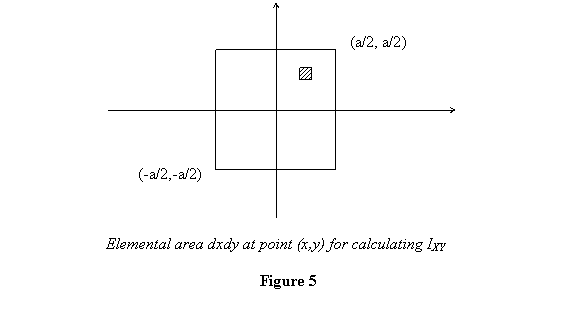
Let us also calculate the product of inertia. Choose on
elemental area dxdy and calculate (see figure
5)
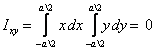
As noted earlier, IYX is
equal to IXY and
therefore it also vanishes.
A related problem is that of a rectangular area of size
a x b.
Its length of side a is parallel to the x-axis
and the other side of length b is parallel to
the y-axis. I leave this as an exercise for you to show
that in this case 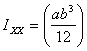 , , 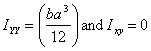 .
Notice that due to the area being symmetrically distributed
about the x- and y-axes, the product of the area comes
out to be zero. .
Notice that due to the area being symmetrically distributed
about the x- and y-axes, the product of the area comes
out to be zero.
Example 2 : Next let us consider a quarter
of an ellipse as shown in figure 6 and calculate the
moment and product of area for this area.
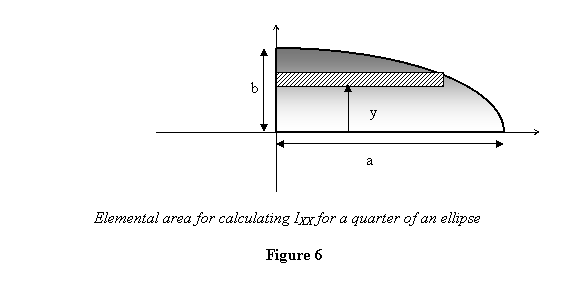
Equation of the ellipse whose quarter is shown in figure
6 is: 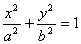 .
For calculating .
For calculating 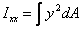 choose
an area element parallel to the x-axis to calculate dA=xdy and
perform the integral choose
an area element parallel to the x-axis to calculate dA=xdy and
perform the integral

Using the equation for ellipse, we get
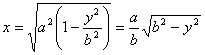
which gives
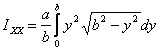
This integral can easily be performed by substituting y
= b sin θ and gives
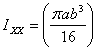
Similarly by taking a vertical strip to perform the integral,
we calculate
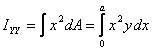
and get
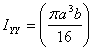
Next we calculate the product of area IXY .
To calculate IXY ,
we take a small element ( 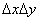 )
as shown in figure 7, multiply it by x and y and
integrate to get )
as shown in figure 7, multiply it by x and y and
integrate to get
 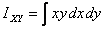
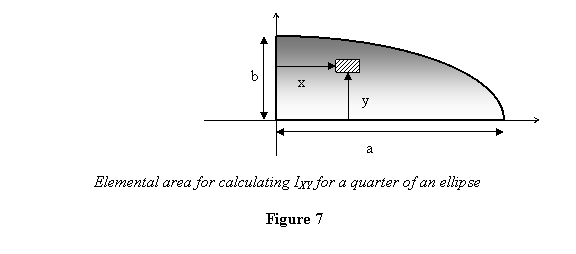
For a given x , the value of y changes
from 0 to 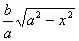 so
the integral is so
the integral is
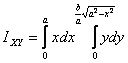
This integral is easily performed to get
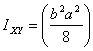
Thus for a quarter of an ellipse, the moments and products
of area are
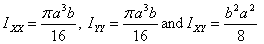
If we put a = b , these formulas give the
moments and products of area for a quarter of a circle
of radius a .
I will leave it for you to work out what will be 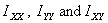 for
the full ellipse about its centre. for
the full ellipse about its centre.
Using the second moment of an area, we define the concept
of the radii of gyration. This is the point which will
give the same moment of inertia as the area under consideration
if the entire area was concentrated there. Thus
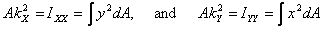
define the radii of gyration kX and kY about
the x- and the y-axes, respectively. In the example of
a rectangular area of size a x b with
side a parallel to the x-axis, we had 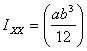 , , 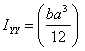 .
So for this rectangle, the radii of gyration are .
So for this rectangle, the radii of gyration are 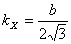 and and 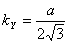 . .
Having defined the moments and products of area, we now
describe a relationship between the second moment of
an area about a set of axes passing through the centroid
of that area and another set of (x-y) axes which are
parallel to those passing through the centroid. This
is known a transfer theorem.
|