Lecture 9
Properties of surfaces II: Second moment of area

Just as we have discussing first moment of an area and its relation with problems in mechanics, we will now describe second moment and product of area of a plane. In this lecture we look at these quantities as some mathematical entities that have been defined and solve some problems involving them. The usefulness of related quantities, called the moments of inertia and products of inertia will become clear when we deal with rotation of rigid bodies.

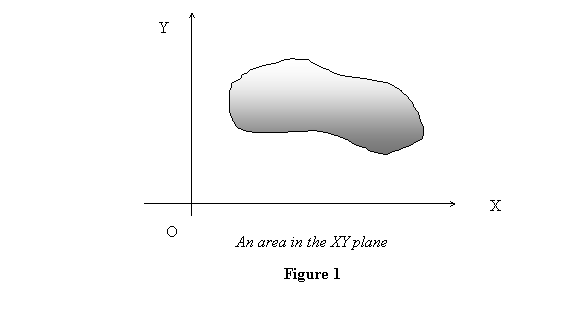
Let us then consider a plane area in xy plane (figure 1). The second moments of the area A is defined as

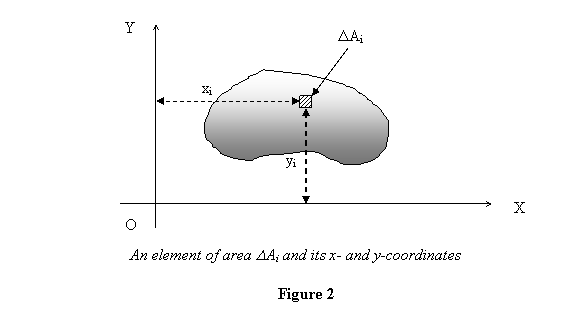
That is given a plane surface, we take a small area in it, multiply by its perpendicular distance from the x-axis and sum it over the entire area. That gives I_XX . Similarly I_YY is obtained by multiplying the small area by square of the distance perpendicular to the y-axis and adding up all contributions (see figure 2).

The product of area is defined as

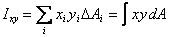
where x and y are the coordinates of the small area dA . Obviously I_XX is the same as I_XY .