As the next example of the application of the concepts developed, we wish to calculate forces on plane rectangular surfaces submerged in water.

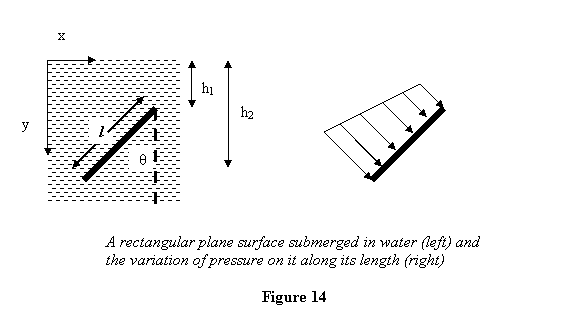
Plane surface Submerged in water: Two questions we wish to answer are (i) What is the average pressure on the plate? and (ii) where does the total force due to the pressure act? Consider a rectangular plate of length l and width w submerged in water at an angle θ from the vertical as shown in figure 14. The upper end of the plate is at the depth of h₁ and the lower one at the depth of h₂ .

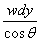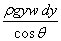We first calculate the average pressure on the plate. At a depth y the pressure acting on the plate is ρgy , where ρ is the density of water and g the gravitational acceleration. If we now take a thin strip of width dy at depth y parallel to the plate's width, its area dA = , and the force on it would be dF = . The total force on the plate would therefore be

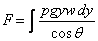
This gives the average pressure to be

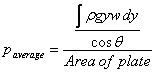
To understand the significance of the expression above better, let us introduce another length variable Y along the plate (see figure 15).

Then we have 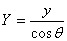so that we can write the average pressure as

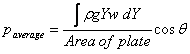
However, 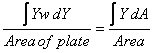is the Y-distance of the centroid of the plate. Let us call it Y_C . Thus

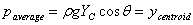
Or the average pressure on the plate is ρg( the depth of the centroid of the plate ). We point out that although we derived this result here for a rectangular plate, the result for the average pressure that 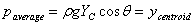is true for a planar surface of any shape. This is because 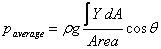  and 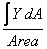is the Y-distance of the centroid of an area of any shape.

Question that we ask now is: at what point does the total force act? To see this let us calculate the moment of the distributed forces due to the pressure. This is given by

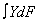
where

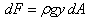
For a rectangular plate, 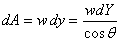, which is independent of Y. So the loading intensity (force per unit length) for a rectangular plate is going to have the same dependence on the depth as the pressure. Thus the loading on a rectangular plate is trapezoidal as shown in figure 14. The Y-coordinate of the point at which the force acts is

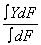
This by definition is the centroid of the area formed by the loading intensity curve. You have already calculated the centroid of a trapezoidal loading curve. Using that result we find that the total force acts at a depth of

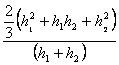
Using this result we now solve one example.

Example 4: A two meter high water tank has an opening of the size 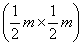at the bottom. The opening is covered by a door hinged on top, shown by A, and is stopped by a fixed wedge, shown by B, at the bottom (see figure 16). Calculate the force on A and B (a) when tank has water filled up to 1m, and (b) has 25cm of water in it. Weight of the door is 19.6N.

(a)   As derived earlier, the average pressure on the door will be given by the depth of its centroid. The centroid of the square is at a depth of (0.5 + 0.25 = 0.75m) from the surface of the water. Thus the average pressure is

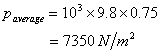
Thus the total force is

F=7350 × .25m 2 =1837.5 N

Notice that having derived our general result for the average pressure earlier, we do not have to perform any integration again to calculate the total force; it is simply the average pressure times the total area. The force is acting at a depth of

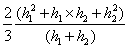
In the present case h₁ = 0.5m , h₂ = 1.0m . This gives that the total force is acting at a depth of 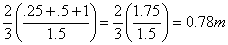or 0 .28m below A. Thus the free body diagram of the door looks as follows

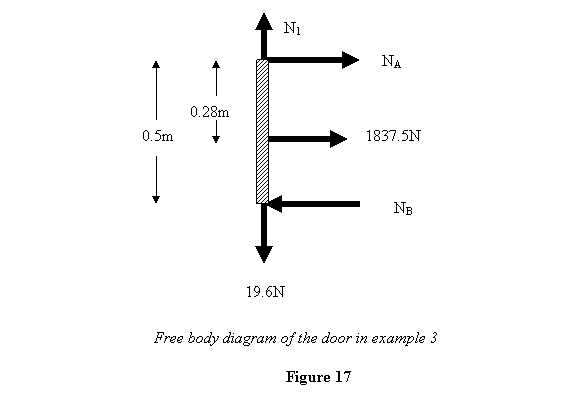
From the force balance equations we have

N_A +N_B = 1837.5

and

N₁ = 19.6N

The torque balance equation, on the other hand, gives

.5N B = .28 x 1837.5

This leads to N_B = 1029 N . Putting this in the force balance equation above gives N_A = 805.5 N. Thus all the forces have been calculated.

(b) In the second case, the pressure works only on a part of the door and the loading due to the pressure is triangular. Having given this lead to the solution, I'll leave the rest of the problem for you to work out. The answers are N_A = 25.425 N, N_B = 127.7 N and N₁ = 19.6 N.

To summarize, in this lecture we have looked at some properties a plane and used it in statics problems. In the next lecture we will expand on this and develop concepts of moment of area and products of area etcetera.