Now let us make one observation: If a body is made up of different shapes of surfaces whose centroid are known. Than the centroid of the composite body

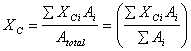
where X_Ci are the centroid of different surfaces and A_i their area. I will leave the simple proof for you, but solve a couple of examples to show you how to use this observation.

 

Example1: Let us take a square of side a and on its two sides let there be two equilateral triangle stuck on it (see figure 7). We wish to calculate the centroid for this surface.

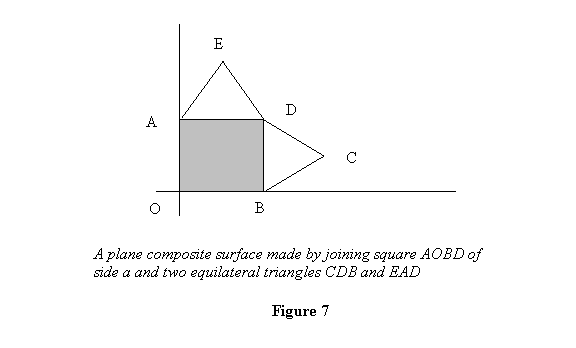
We will consider this body as composed of the square AOBD, the triangle CDE on its right CDE and triangle EAD on its top. Then for the square we have

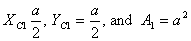
For the triangle on the right of the square

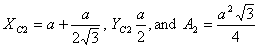
And for the triangle on top of the square

.

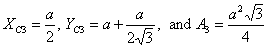Thus for the entire plane we get

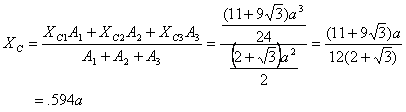
Similarly

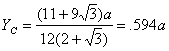
So because of the triangles, the centroid shift a bit to the right and a bit up with respect to the centroid of the square; this happens because of the added area of the triangles.

 

Example 2: As the second example, let us take an area (ABCDE) that has been obtained by removing a semicircular area from a square. We wish to find its centroid.

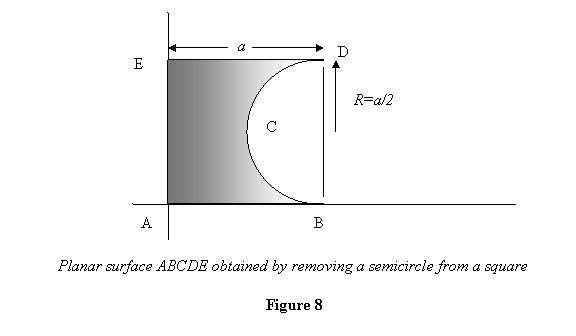
We know the position of the centroid of the square and the semicircular area. Thus

 

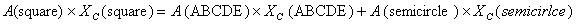
Therefore

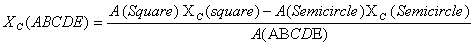
From the previous calculation, we know that the centroid for semicircle is

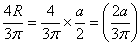
from the base. So In the present case we have

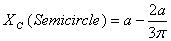
The centroid of the figure ABCDE is then

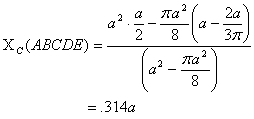
which is a little more than 0.25a . If we had removed a rectangular area equal to half the square, the X C for the area left would have been at 0.25a ; because of the extra area to the right of this point when the semicircle is removed, the centroid shifts slightly to the right.

After introducing you to the mathematical concepts of the first moment and centroid of a surface area, we now apply these ideas to problems in mechanics.