Application to mechanics: As the first simple application of the methods developed let us consider beams which are externally loaded. We consider only those situations where beams are supported externally so that the external reactions can be calculated on the basis of statics alone. As in the case of trusses, such beams are called statically determinate beams. Now one such beam is loaded externally between X₁ and X₂ as shown in figure 9.

 

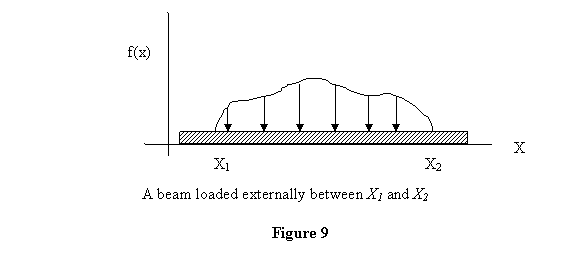
In the figure the function f(x) is the load intensity which is equal to load per unit length. Thus force over a length dx is given by dF = f(x) dx . The total load R therefore is

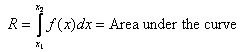
Next question we ask is where is the total load located? This is determined by finding the Moment (torque) created by the load, which is given by

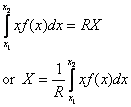
Thus the location of the load is given by the centroid of the area formed by the load curve and the beam, taking beam as the x-axis. Let us now take some examples.

 

Uniform loading: This is shown in figure 10 along with the total load R acting at the centroid of the loading intensity curve. The uniform load intensity is w .

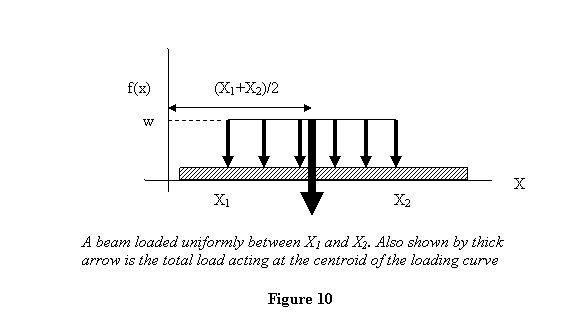
The total load in this case is 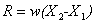and the load acts at the centroid

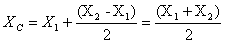
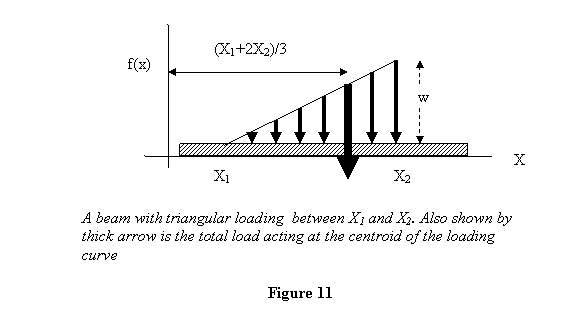
Triangular loading : This is shown in figure 11 along with the total load R acting at the centroid of the loading intensity curve. The height of the triangle is w .

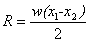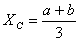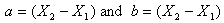In this case the total load is and the load acts at the centroid of the triangle. Recall that for a triangle from the lower left vertex (figure 4) and in the present case . Therefore the centroid is at

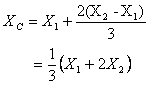
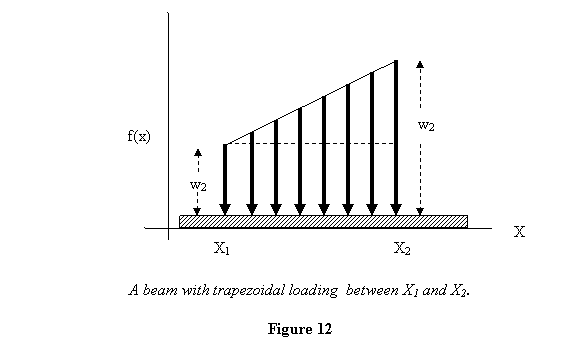
I will leave the case of trapezoidal loading (shown in figure 12) for you to work out. You may wish to consider this loading as made up of two different ones: the lower one a rectangular and the upper one a triangular loading.