Centroid: Centroid of
a bounded area is a point whose x-coordinates XC and
y-coordinate YC are defined as
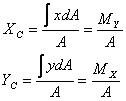
where A is its total area. We now solve
some examples of calculating these quantities for
some simple areas.
Example 1: We start with the simple
example of the first moment and centroid of a triangle
with the base along the x-axis. Let its base BC be
of length b, and let the height of the
triangle be h. (see figure 3)
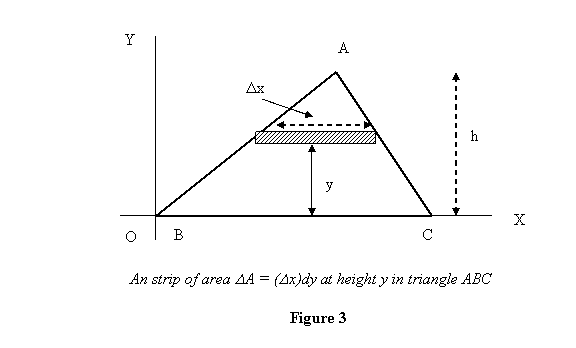
To calculate the Mx, we take a strip of
width dy at height y (see figure
3). Then
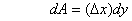
But by similarity of triangles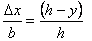 
.
So
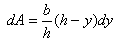
Thus
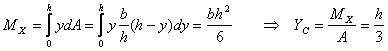
Let us now calculate the x-co-ordinates for the centroid.
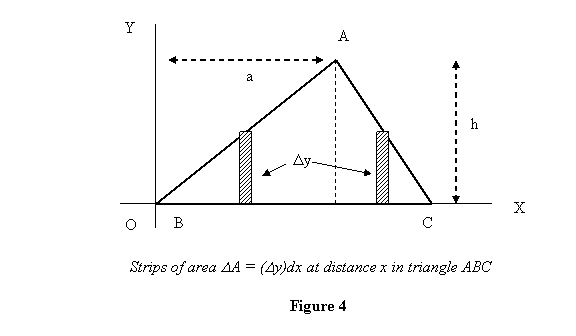
For this let the x-coordinate of A be a so
that the coordinate of point A is (a, h).
Now
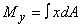
For dA let us now take a vertical strip
(figure 4). Notice that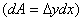 
.
We will also perform the x-integration in two parts:
one from x = 0 to x = a, and the other from x = a
to x = b because in the two regions, dependent of y on x is
different so
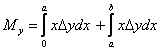
For the region x = 0 to x = a, we can write
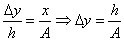
and for the region x = a to x = b, we have
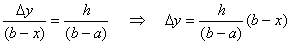
Thus
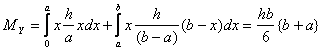
This gives
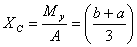
Thus for a triangle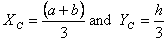 
.
Example2: As the second example,
let us calculate the centroid of a semicircular disc
of radius R . It would be quite easy to
solve this problem if the centre D of the
circle is kept at the origin but I want to do the
problem with the disc positioned as drawn below to
show you how to tackle the problem.
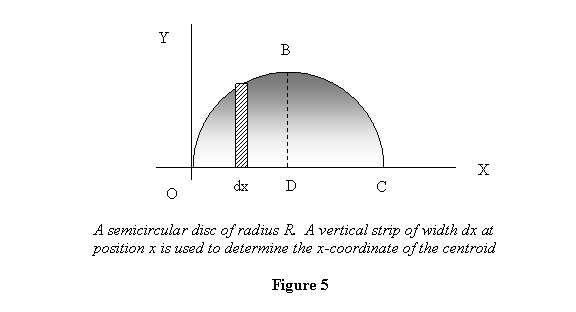
The equation of OBC (the circular boundary of the
disc) is
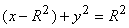
where R is the radius of the circle. The
total area of the plate is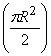 
.
To calculate XC , we take a vertical strip
of width dx at x and calculate
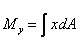
With
,
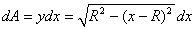we get
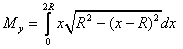
To evaluate this integral, we let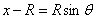 
so
that the limits of θ integration are from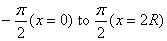 
.
Then
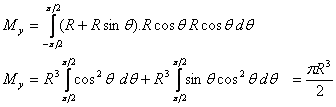
which gives
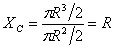
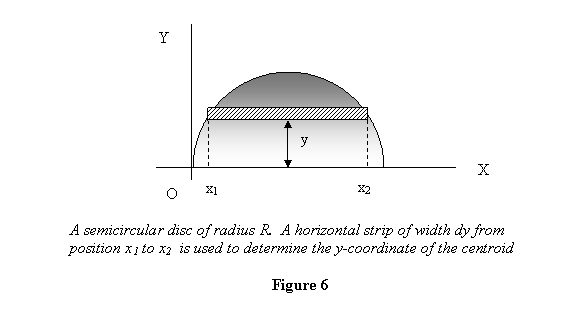
To calculate YC we need to calculate MX =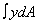 
,
where dA represents as strip from x1 to x2 (see
figure 6)
From the equation of the circle we get
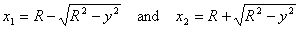
This gives
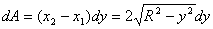
and therefore
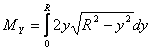
Substituting y = R sin θ , we get
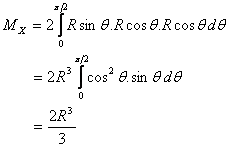
This gives
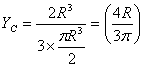
Thus the centroid of the semicircle shown is at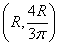 
.
Notice that the y coordinate of the centroid is less
than 
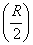which
is easily understood because more of the area is
concentrated towards the x-axis.
We would no like to emphasize that the centroid (XC
YC ) gives a point fixed in a given
planar surface and no matter in which co-ordinate
system we calculate this point, it will always
come out to be the same point in the surface.
Thus it is a property of a surface.
