Method of sections : As the name
suggests in method of sections we make sections
through a truss and then calculate the force in the members
of the truss though which the cut is made. For
example, if I take the problem we just solved in the
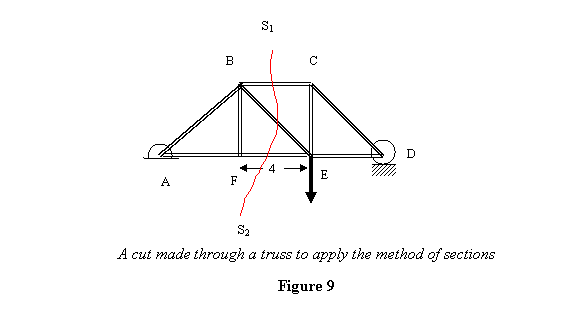
method of joints and make a section S1, S2
(see figure 9), we will be able to determine the forces
in members BC, BE and FE by considering the equilibrium
of the portion to the left or the right of the section.
Let
me now illustrate this. As in the method of joints,
we start by first determining the reactions at the
external support of the truss by considering it as
a whole rigid body. In the present particular case,
this gives 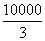 N at
D and
N at
D and 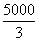 N at
A. Now let us consider the section of the truss on
the left (see figure 10).
N at
A. Now let us consider the section of the truss on
the left (see figure 10).
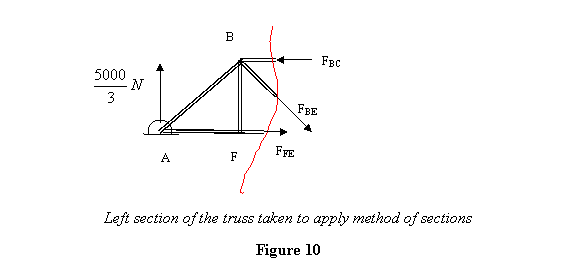
Since this entire section is in equilibrium, 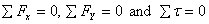 .
Notice that we are now using all three equations
for equilibrium since the forces in individual members
are not concurrent. The direction of force in each
member, one can pretty much guess by inspection.
Thus the force in the section of members BE must
be pointing down because there is no other member
that can give a downward force to counterbalance
.
Notice that we are now using all three equations
for equilibrium since the forces in individual members
are not concurrent. The direction of force in each
member, one can pretty much guess by inspection.
Thus the force in the section of members BE must
be pointing down because there is no other member
that can give a downward force to counterbalance 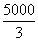 N reaction
at A. This clearly tells us that F BE is
tensile. Similarly, to counter the torque about B
generated by
N reaction
at A. This clearly tells us that F BE is
tensile. Similarly, to counter the torque about B
generated by 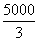 N force
at A, the force on FE should also be from F to E.
Thus this force is also tensile. If we next consider
the balance of torque about A,
N force
at A, the force on FE should also be from F to E.
Thus this force is also tensile. If we next consider
the balance of torque about A, 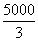 N
and FFE do not give any torque about A.
So to counter torque generated by FBE , the force
on BC must act towards B, thereby making the force
compressive.
N
and FFE do not give any torque about A.
So to counter torque generated by FBE , the force
on BC must act towards B, thereby making the force
compressive.
Let us now calculate individual forces. FFE is easiest
to calculate. For this we take the moment about B.
This gives
4 × 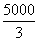 =
4 × F FE
=
4 × F FE
F FE = 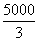 N
N
Next we calculate FBE . For this, we use the equation 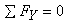 .
It gives
.
It gives
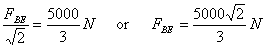
Finally to calculate FBC , we can use either
the equation 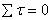 about
A or
about
A or 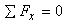
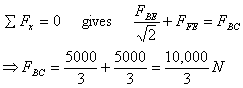
Thus we have determined forces in these three members
directly without calculating forces going from one
joint to another joint and have saved a lot of time
and effort in the process. The forces on the right
section will be opposite to those on the left sections
at points through which the section is cut. This
can be used to check our answer, and I leave it as
an exercise for you.
After this illustration let me put down the steps
that are taken to solve for forces in members of
a truss by method of sections:
- Make a cut to divide the truss into section,
passing the cut through members where the force
is needed.
- Make the cut through three member of a truss
because with three equilibrium equations viz.
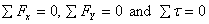 we
can solve for a maximum of three forces.
we
can solve for a maximum of three forces.
- Apply equilibrium conditions and solve for the
desired forces.
In applying method of sections, ingenuity lies in
making a proper. The method after a way of directly
calculating desired force circumventing the hard
work involved in applying the method of joints where
one must solve for each joint.
We thus conclude one lecture or trusses. Next step
in making the treatment accurate is obviously to
take care of deformation in the members of a truss.
This will be done in an advanced course later.