Lecture
7
Friction
Whatever we have studied so far, we have always taken
the force applied by one surface on an object to be normal
to the surface. In doing so, we have been making an approximation
i.e., we have been neglecting a very important force
viz., the frictional force. In this lecture we look at
the frictional force in various situations.
In this lecture when we talk about friction, we would
mean frictional force between two dry surfaces. This
is known as Coulomb friction. Frictional forces also
exist when there is a thin film of liquid between two
surfaces or within a liquid itself. This is known as
the viscous force. We will not be talking about such
forces and will focus our attention on Coulomb friction
i.e., frictional forces between two dry surfaces only.
Frictional force always opposes the motion or tendency
of an object to move against another object or against
a surface. We distinguish between two kinds of frictional
forces - static and kinetic - because it is observed
that kinetic frictional force is slightly less than maximum
static frictional force.
Let us now perform the following experiment.
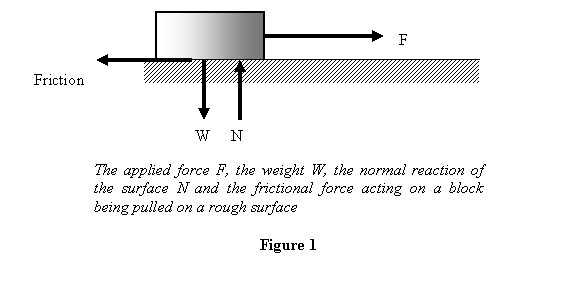
Put a block on a rough surface and pull it by a force F (see
figure 1). Since the force F has a tendency
to move the block, the frictional force acts in the opposite
direction and opposes the applied force F.
All the forces acting on the block are shown in figure
1. Note that I have shown the weight and the normal reaction
acting at two different points on the block. I leave
it for you to think why should the weight and the normal
reaction not act along the same vertical line?
It is observed that the block does not
move until the applied force F reaches a maximum
value Fmax. Thus from F = 0 up to F
= Fmax,
the frictional force adjusts itself so that it is just
sufficient to stop the motion. It was observed by Coulombs
that F max is proportional to the
normal reaction of the surface on the object. You can
observe all this while trying to push a table across
the room; heavier the table, larger the push required
to move it. Thus we can write
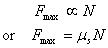
where µs is known as the coefficient
of static friction. It should be emphasize again that
is the maximum possible value of frictional force, applicable
when the object is about to stop, otherwise frictional
force could be less than, just sufficient to prevent
motion. We also note that frictional force is independent
of the area of contact and depends only on N .
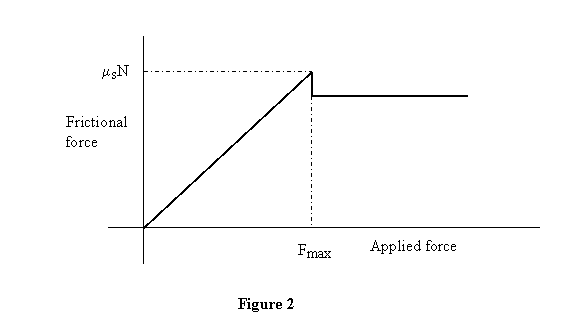
As the applied force F goes
beyond F ,
the body starts moving now experience slightly less force
compound to. This force is seem to be when is known as
the coefficient of kinetic friction. At low velocities
it is a constant but decrease slightly at high velocities.
A schematic plot of frictional force F as a
function of the applied force is as shown in figure 2.
Values of frictional coefficients for different materials
vary from almost zero (ice on ice) to as large as
0.9 (rubber tire on cemented road) always remaining
less than 1.
A quick way of estimating the value of static friction
is to look at the motion an object on an inclined
plane. Its free-body diagram is given in figure 3.
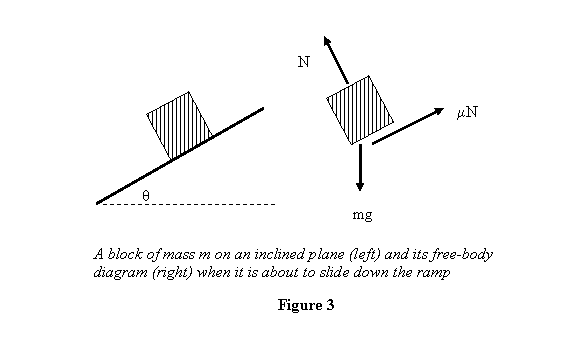
Since the block has a tendency to slide down, the
frictional force points up the inclined plane. As
long as the block is in equilibrium
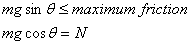
As θ is increased,
mgsinθ increases
and when it goes past the maximum possible value
of friction fmax the block starts sliding down.
Thus at the angle at which it slides down we have
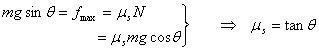
|