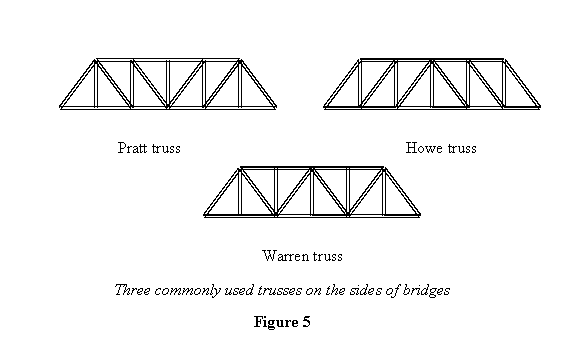
Exercise 1: Shown in figure 5 are three commonly used trusses on the sides of bridges. Show that all three of them are simple trusses.

You may ask why we put trusses on bridges. As our later analysis will show they distribute the load over all elements and thereby making the bridge stronger.

We now wish to obtain the forces generated in various arms of a truss when it is loaded externally. This is done under the following assumptions:

1. If the middle line of the members of a truss meet at a point that point is taken as a pin joint. This is a very god assumption because as we have seen earlier while introducing a truss (triangle with pin joint), the load is transferred on to other member of the trusses so that forces remain essentially collinear with the member.
2. All external loads are applied on pin connections.
3. All members' weight is equally divided on connecting pins.

There are two methods of determining forces in the members of a truss - Method of joints and method of sections. We start with the method of joints:

Method of joints: In method of joints, we look at the equilibrium of the pin at the joints. Since the forces are concurrent at the pin, there is no moment equation and only two equations for equilibrium viz. 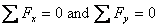. Therefore we start our analysis at a point where one known load and at most two unknown forces are there. The weight of each member is divided into two halves and that is supported by each pin. To an extent, we have already alluded to this method while introducing trusses. Let us illustrate it by two examples.

Example 1: As the first example, I take truss ABCDEF as shown in figure 6 and load it at point E by 5000N. The length of small members of the truss is 4m and that of the diagonal members is 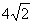m. I will now find the forces in each member of this truss assuming them to be weightless.

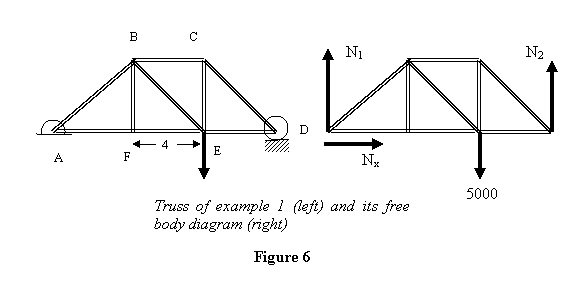
We take each point to be a pin joint and start balancing forces on each of the pins. Since pin E has an external load of 5000N one may want to start from there. However, E point has more than 2 unknown forces so we cannot start at E. We therefore first treat the truss as a whole and find reactions of ground at points A and D because then at points A and D their will remain only two unknown forces. The horizontal reaction Nx at point A is zero because there is no external horizontal force on the system. To find N₂ I take moment about A to get

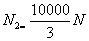
which through equation gives

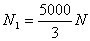
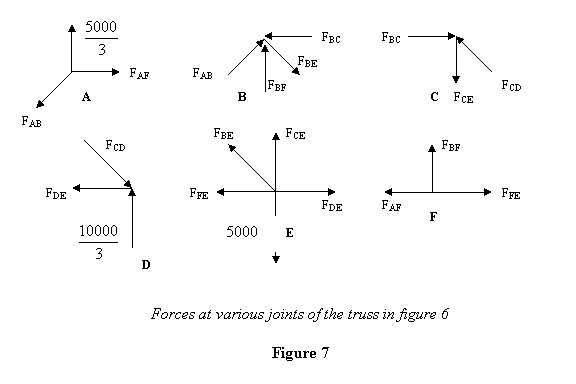
In method of joints, let us now start at pin A and balance the various forces. We already anticipate the direction and show their approximately at A (figure 7). All the angles that the diagonals make are 45° .

The only equations we now have worry about are the force balance equations.

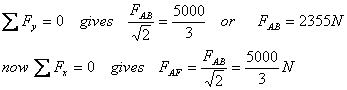
Keep in mind that the force on the member AB and AF going to be opposite to the forces on the pin ( Newton 's III^rd law). Therefore force on member AB is compressive (pushes pin A away) whereas that on AF is tensile (pulls A towards itself).

Next I consider joint F where force AF is known and two forces BF and FE are unknown. For pint F

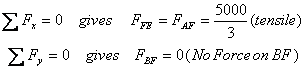
Next I go to point B since now there are only two unknown forces there. At point B

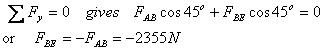
Negative sign shows that whereas we have shown F_BE to be compressive, it is actually tensile.

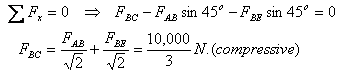
Next I consider point C and balance the forces there. I have already anticipated the direction of the forces and shown F_CE to be tensile whereas F_CD to be compressive

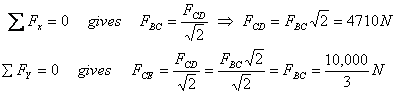
Next I go to pin D where the normal reaction is 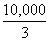N and balance forces there.

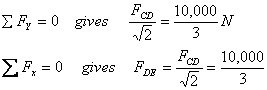
Thus forces in various members of the truss have been determined. They are

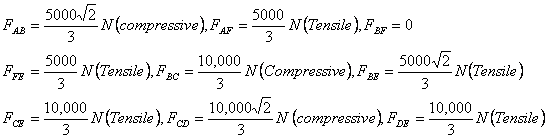
You may be wondering how we got all the forces without using equations at all joints. Recall that is how we had obtained the statical determinacy condition. We did not have to use all joints because already we had treated the system as a whole and had gotten two equations from there. So one joint - in this case E - does not have to be analyzed. However, given that the truss is statically determinate, all these forces must balance at point E, where the load has been applied, also. I will leave this as an exercise for you. Next I ask how the situation would change if each member of the truss had weight. Suppose each members weighs 500N, then assuming that the load is divided equally between two pins holding the member the loading of the truss would appear as given in figure 8 (loading due to the weight as shown in red). Except at points A and D the loading due to the weight is 750N; at the A and D points it is 500N.

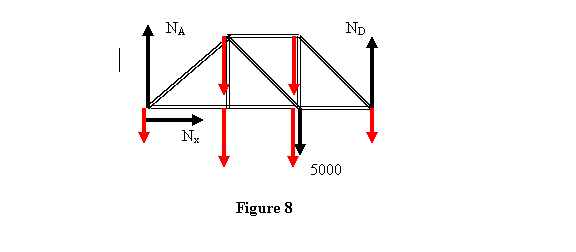
Now the external reaction at each end will be.

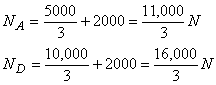
The extra 2000N can be calculated either from the moment equation or straightaway by realizing that the new added weight is perfectly symmetric about the centre of the truss and therefore will be equally divided between the two supports. For balancing forces at other pins, we follow the same procedure as above, keeping in mind though that each pin now has an external loading due to the weight of each member. I'll solve for forces in some member of the truss. Looking at pin A, we get

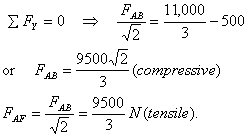
Next we move to point F and see that the forces are

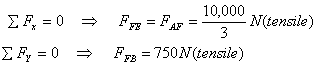
One can similarly solve for other pins in the truss and I leave that as an exercise for you.

Having demonstrated to you the method of joints, we now move on to see the method of sections that directly gives the force on a desired member of the truss.