Lecture 6
Trusses

Having set up the basics for studying equilibrium of bodies, we are now ready to discuss the trusses that are used in making stable load-bearing structures. The examples of these are the sides of the bridges or tall TV towers or towers that carry electricity wires. Schematic diagram of a structure on the side of a bridge is drawn in figure 1.

The structure shown in figure 1 is essentially a two-dimensional structure. This is known as a plane truss. On the other hand, a microwave or mobile phone tower is a three-dimensional structure. Thus there are two categories of trusses - Plane trusses like on the sides of a bridge and space trusses like the TV towers. In this course, we will be concentrating on plane trusses in which the basis elements are stuck together in a plane.

To motivate the structure of a plane truss, let me take a slender rod (12) between points 1 and 2 and attach it to a fixed pin joint at 1 (see figure 2).

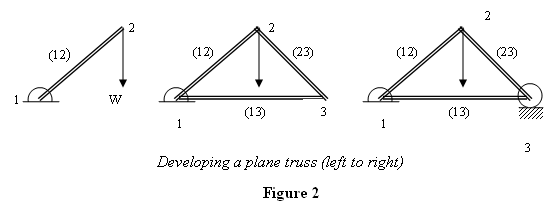
Now I put a pin (pin2) at point 2 at the upper end and hang a weight W on it. The question is if we want to hold the weight at that point, what other minimum supports should we provide? For rods we are to make only pin joints (We assume everything is in this plane and the structures does not topple side ways). Since rod (12) tends to turn clockwise, we stop the rightward movement of point 2 by connecting a rod (23) on it and then stop point 3 from moving to the right by connecting it to point 1 by another rod (13). All the joints in this structure are pin joints. However, despite all this the entire structure still has a tendency to turn to turn clockwise because there is a torque on it due to W. To counter this, we attach a wheel on point 3 and put it on the ground. This is the bare minimum that we require to hold the weight is place. The triangle made by rods forms the basis of a plane truss.

Note: One may ask at this point as to why as we need the horizontal rod (13). It is because point 3 will otherwise keep moving to the right making the whole structure unstable. Rod (13) has two forces acting on it: one vertical force due to the wheel and the other at end 2. However these two forces cannot be collinear so without the rod (13) the system will not be in equilibrium. Generally, in a truss each joint must be connected to at least three rods or two rods and one external support.

Let us now analyze forces in the structure that just formed. For simplicity I take the lengths of all rods to be equal. To get the forces I look at all the forces on each pin and find conditions under which the pins are in equilibrium. The first thing we note that each rod in equilibrium under the influence of two forces applied by the pins at their ends. As I discussed in the previous lecture, in this situation the forces have to be collinear and therefore along the rods only. Thus each rod is under a tensile or compressive force. Thus rods (12), (23) and (13) experience forces as shown in figure 3.

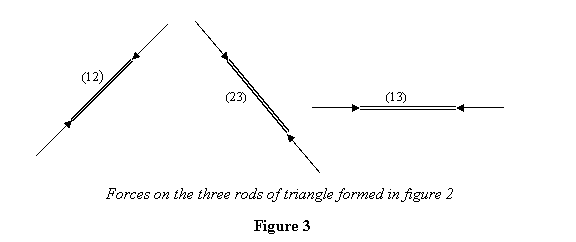
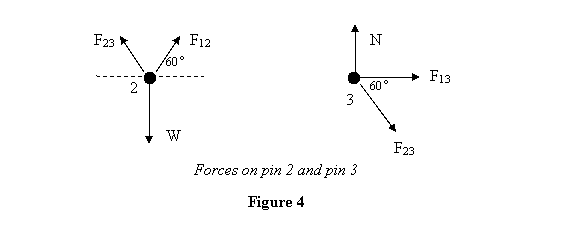
Notice that we have taken all the forces to be compressive. If the actual forces are tensile, the answer will come out to be negative. Let us now look at pin 2. The only forces acting on pin 2 are F₁₂ due to rod (12) and F₂₃ due to rod (23). Further, it is pulled down by the weight W. Thus forces acting on pin 2 look like shown in figure 4.

Applying equilibrium condition to pin (2) gives

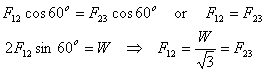
Let us now look at pin 3 (see figure 4). It is in equilibrium under forces F₂₃, normal reaction N and a horizontal force F₁₃.

Applying equilibrium condition 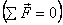gives

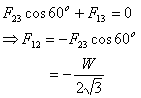
Since the direction of F₁₃ is coming out to be negative, the direction should be opposite to that assumed. Balance of forces in the vertical direction gives

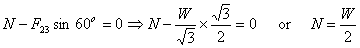
Thus we see that the weight is held with these three rods. The structure is determinate and it holds the weight in place.

Even if we replace the pin joints by a small plate (known as gusset plate) with two or three pins in these, the analysis remains pretty much the same because the pins are so close together that they hardly create any moment about the joints. Even if the rods are welded together at the joints, to a great degree of accuracy most of the force is carried longitudinally on the rods, although some very small (negligible) moment is created by the joints and may be by possible bending of the rods.

Now we are ready to build a truss and analyze it. We are going to build it by adding more and more of triangles together. As you can see, when we add these triangles, the member of joints j and the number of members (rods) m are related as follows:

m = 2j - 3

This makes a truss statically determinate. This is easily understood as follows. First consider the entire truss as one system. If it is to be statically determinate, there should be only three unknown forces on it because for forces in a plane there are three equilibrium conditions. Fixing one of its ends a pin joint and putting the other one on a roller does that (roller also gives the additional advantage that it can help in adjusting any change in the length of a member due to deformations). If we wish to determine these external forces and the force in each member of the truss, the total number of unknowns becomes m + 3. We solve for these unknowns by writing equilibrium conditions for each pin; there will be 2j such equations. For the system to be determinate we should have m + 3 = 2j , which is the condition given above. If we add any more members, these are redundant. On the other hand, less number of members will make the truss unstable and it will collapse when loaded. This will happen because the truss will not be able to provide the required number of forces for all equilibrium conditions to be satisfied. Statically determinate trusses are known as simple trusses.