Let me now summarize what all you have learnt so far in considering the equilibrium of engineering structures. In the process I also introduce you to a term called the Free Body Diagram. I have actually been using it without calling it so. Now, let us formalize it.

In talking about the equilibrium of a body we consider all the external forces applied on it and the interaction of the body with other objects around it. This interaction produces more forces and torques on the body. Thus when we single out a body in equilibrium, objects like hinges, ball-socket joint, fixed supports around it are replaced elements by the corresponding forces & torques that they generate. This is what is called a free-body diagram. Making a free-body diagram allows us to focus our attention only on the information relevant to the equilibrium of the body, leaving out unnecessary details. Thus making a free-body diagram is pretty much like Arjuna - when asked to take an aim on the eye of a bird - seeing only the eye and nothing else. The diagrams made on the right side of figures 1, 2 and 3 are all free-body diagrams.

In the coming lecture we will be applying the techniques learnt so far to a very special structure called the truss. To prepare you for that, in the following I consider the special case of a system in equilibrium under only two forces. For completeness I will also take up equilibrium under three forces.

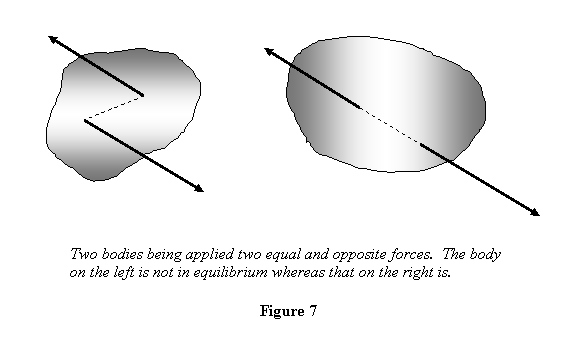
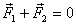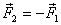When only two forces are applied, no matter what the shape or the size of the object in equilibrium is, the forces must act along the same line, in directions opposite to each other, and their magnitudes must be the same. That the forces act in directions opposite to each other and have equal magnitude follows from the equilibrium conditions , which implies that . Further, if the forces are not along the same line then they will form a couple that will tend to rotate the body. Thus 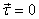implies that the forces act along the same line, i.e. they be collinear (see figure 7).

Similarly if there are three forces acting on a body that is in equilibrium then the three forces must be in the same plane and concurrent. If there are not concurrent then they must be parallel (of course remaining in the same plane). This can be understood as follows. Any two members of the three applied forces form a plane. If the third force is not in the same plane, it will have a non-vanishing component perpendicular to the plane; and that component does not get cancelled. Thus unless all three forces are in the same plane, they cannot add up to zero. So to satisfy the equation 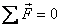, the forces must be in the same plane, i.e. they must be coplanar. For equilibrium the torque about any point must also be zero. Since the forces are in the same plane, any two of them will intersect at a certain point O. These two forces will also have zero moment about O. If the third force does not pass through O, it will give a non-vanishing torque (see figure 8). So to satisfy the torque equation, the forces have to be concurrent. Zero torque condition can also be satisfied if the three forces are parallel forces (see figure 8); that is the other possibility for equilibrium under three forces.

In the end, I now discuss one more concept about equilibrium of bodies, that of statical determinacy . Along the way I also introduce some connected concepts like constraints, degree of redundancy and redundant support. On constraints, I will discuss more in the lecture on Method of virtual work.

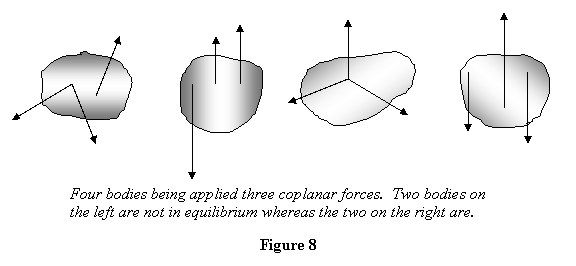
To introduce the terms used above, I consider a rod of length l and weight W held at a pin-joint on a floor at a distance of a from a wall, on which its other end is. This is shown in figure 9 along with the free-body diagram of the rod.

There are three unknowns - Rx, Ry and N - in the problem and three equations of equilibrium that will determine the unknowns. Specifically:

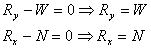
Taking moment about the pin, we get

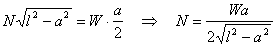
This gives

 

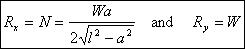
In this case, the constraints or the external supports we apply are just sufficient to keep the system in equilibrium. Such systems are known as statically determinate systems. Now suppose we apply one more support. Let us support the rod at both ends by pin joints. The free-body diagram will then look like that shown in figure 10.

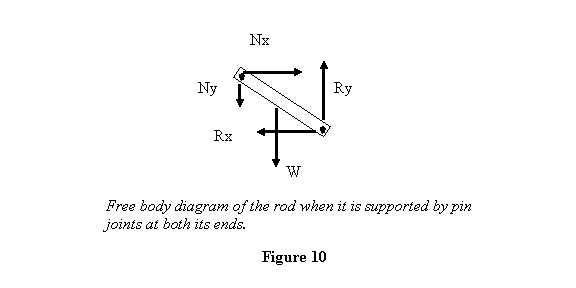
Now the pin on top end is also applying a force on the rod. Thus the equations of equilibrium read as

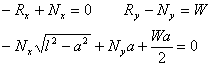
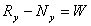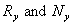The situation on hand is that we have four unknowns - Rx, Ry, Nx and Ny - and only three equations. Thus one of the unknown cannot be determined. In particular only is known and what are individual cannot be determined unless some additional information is also given. Such systems are known as statically indeterminate systems. In such systems we are applying more constraints than are needed to keep the system in equilibrium. Even if we remove one of the constraints - in this case replace the upper pin by a plane surface - the system is capable of remaining in equilibrium. Such supports that can be removed without disturbing the equilibrium are known as redundant supports. And the number of redundant supports is the degree of statical indeterminacy .

After introducing you to the concepts discussed above, we will be studying trusses in the next lecture.