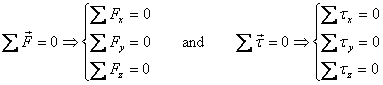In the previous lecture I have been talking about
equilibrium in a plane. We now move on to three dimensional
(3-d) cases. In three dimensional cases
the equilibrium conditions lead to balance along
all three axes. Then
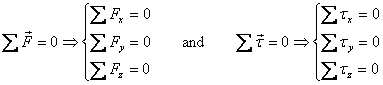
We now have to take care of components of forces and
torque in all three dimensions. The engineering elements
that we considered earlier are now considered as 3-d case.
Thus consider a ball-socket joint in which a ball
is supported in a socket (figure 1).
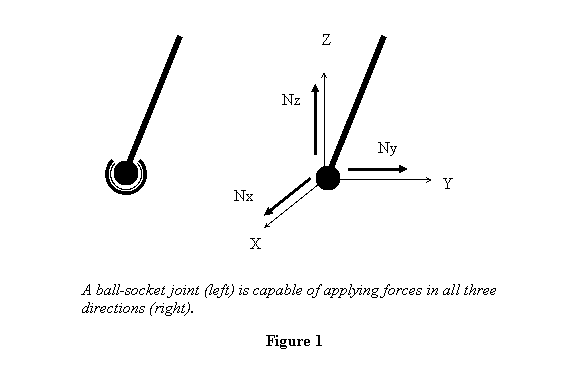
A ball-socket joint provides reaction forces Nx, Ny and Nz in
all three directions (figure 1) but it cannot apply
any torque. This is a little like a hinge joint in 2d .
Let me solve an example using such a joint.
Example 1: To balance a heavy weight
of 5000 N, two persons dig a hole in the
ground and put a pole of length l in it
so that the hole acts as a socket. The pole makes
an angle of 30° from the ground. The weight
is tied at the mid point of the pole and the pole
is pulled by two horizontal ropes tied at its ends
as shown in figure 2. Find the tension in the two
ropes and the reaction forces of the ground on the
pole.
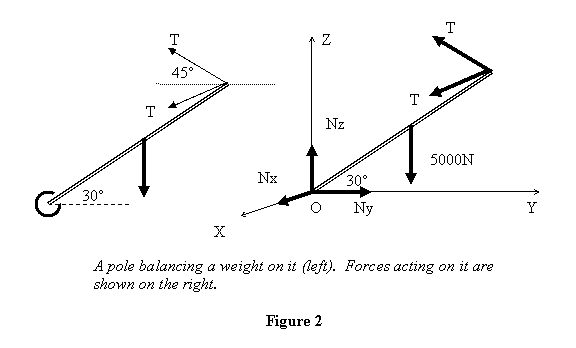
To solve this problem, let me first choose a co-ordinate
system. I choose it so that the pole is over the
y-axis in the (y-z) plane (see figure 2).
The ropes are in (xy) direction with tension T in
each one of them so that tension in each is written
as
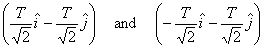
You may be wondering why I have taken the tension
to be the same in the two ropes. Actually it arises
from the torque balance equation; if the tensions
were not equal, their component in the x-direction
will give a nonzero torque.
Let the normal reaction of the ground be (Nx ,
Ny , Nz). Then the force balance
equation gives
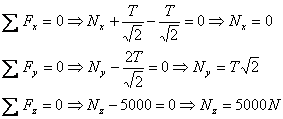
Taking torque about point O and equating it to zero,
we get
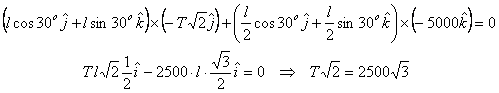
which gives

Next, if I consider a fixed connection, say in a wall,
it is capable of providing force along all the three
axes and also of providing torques about the three
axes, Thus in 3-d it will be represented
as shown in figure 3.
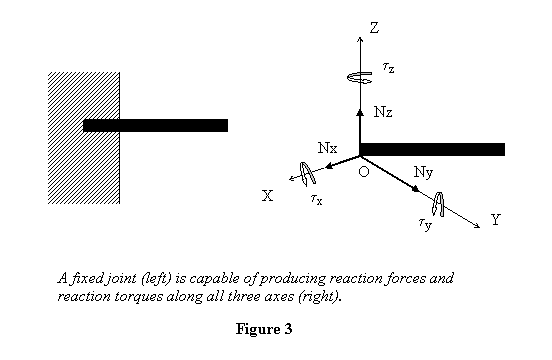
This is a generalization of the fixed or welded/glued
support in 2-d . How are these torques etc.
generated? Recall what I did for a fixed support
in 2-d and carry out a similar analysis
in 3-d.
Hopefully by the analysis carried out so far, you
would be able to recognize what all reactions a given
element of a mechanical system can provide. For example
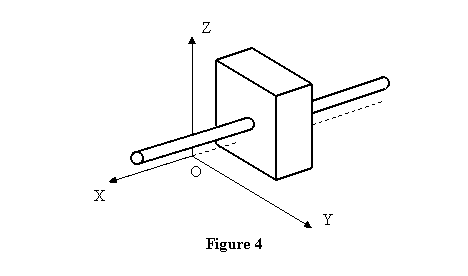
look at the support shown in figure 4 where the shaft
can not move through the hole in the fixed block,
but it is free to rotate. Can you tell the reaction
forces and torques that this support provides?
Having discussed the elements that apply different
kinds of forces, let us look at some situations there
due to the geometry of forces applied, some of the
equilibrium equations are automatically satisfied.
If we recognize this, it saves us from doing extra
calculations involving that particular condition.
If all forces are concurrent at a point (see
figure 5), i.e., they all cross each other at one
point O then torques of all the forces is
identically zero about O . Thus the only
equilibrium condition is
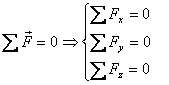
Recall that if the sum of all forces on a system is
zero, torque is independent of the origin. Thus although
in the beginning I used the fact that torque about
the point of concurrence is zero, it is true about
any point once the force equation for equilibrium
is satisfied.
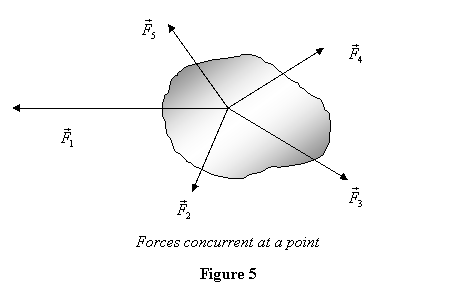
Next consider the case when all forces intersect
one particular line, call it the z-axis
without any loss of generality (see figure 6).
Using transmissibility of the force, in this case
we can take the force 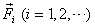 to
be acting at point
to
be acting at point 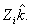 Then
the torque due to all these forces will be
Then
the torque due to all these forces will be
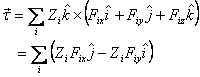
Thus the Z component of the torque is automatically
zero. In general when the forces intersect a line,
the torque component along that line vanishes. Under
these circumstances, if we take that line to be the
z-axis, the equilibrium conditions are
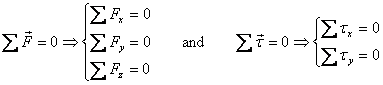
Next I discuss what happens if all the applied forces
are parallel, say to the Z axis. Then the
forces do not have any x or y components.
Further, by the z-component of the torque also vanishes
(left as an exercise for you to show). The equilibrium
conditions in this case reduce to

In general of course we have all the six condition.