Forces and couples generated by various elements: As we solve engineering problems, we come across many different elements that are used in engineering structures. We discuss some of them below focusing our attention on what kind of forces and torques do they give rise to.

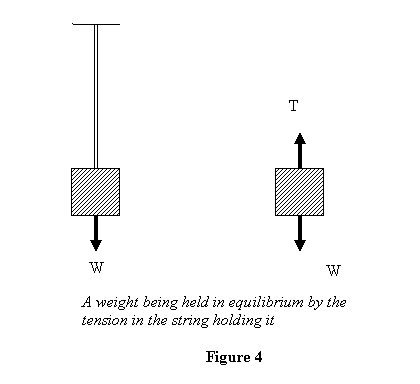
The simplest element is a string that can apply a tension. However a string can only pull by the tension generated in it but not push. For example, a string holding a weight W will develop a tension T = W in it so that the net force on the weight is a tension T pulling the weight up and weight W pulling it down. Thus if the weight is in equilibrium, T = W . This is shown in figure 4.

The second kind of force that is applied when two elements come in contact is that applied by a surface. A smooth surface always applies a force normal to itself. The forces on a rod and on a box applied by the surface are shown in figure 5. Thus as far as the equilibrium is concerned, for an object on a smooth surface, the surface is equivalent to a force normal to it.

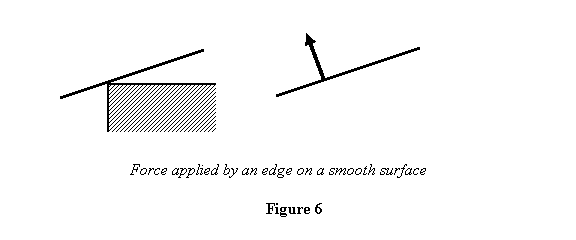
Imagine what would have happened had the force by the surface not been normal. Then an object put on a surface would start moving along the surface because of the component of the force along the surface. By the same argument if there is a smooth surface near an edge, the force on the surface due to the edge (and by Newton's III^rd law the force on the edge due to the surface) will be normal to the surface. See figure 6.

On the other hand if the surface is not smooth, it is then capable of applying a force along the surface also. This force is due to friction.

Let us now solve the well known example of a roller of radius r being pulled over a step as shown in figure 7. The height of the step is h. What is minimum force F required if the roller is pulled in the direction shown and is about to roll over the step. What are the normal and frictional forces at that instant?

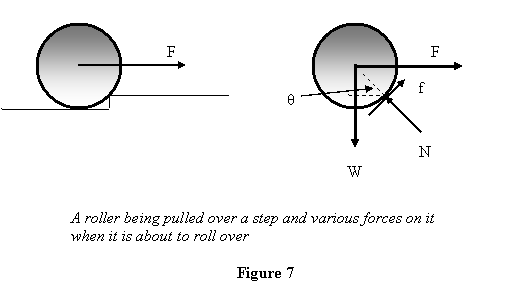
When the roller is about to roll over the step, there will be no normal reaction from the lower surface and therefore the roller will be under equilibrium under the influence of its weight W, the applied force F and the normal reaction N and the frictional force f applied by the edge of the step. To calculate the force F, we apply the torque equation about the edge to get

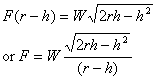
To find N and f we apply the force equation

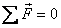
That can be written in the component form a

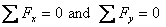
Let us look at these equations.

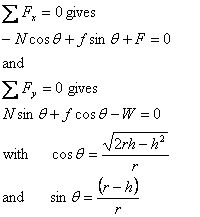
Solving these equations gives

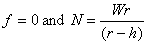
So in this situation, we do not require friction to keep the roller in equilibrium. On the other hand recall the problem in the previous lecture when we were trying to lift a 1000Nt weights by putting a rod on a brick edge. In that case we did require friction.

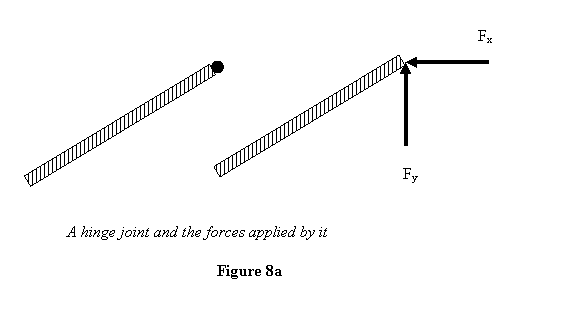
Next we consider a hinge about when an object can rotate freely. A hinge can apply a force in any direction. Thus it can apply (figure 8a) any force in X-direction and any amount of force in Y-direction but no couple.

To see an example, imagine lifting a train berth by pulling it horizontally. We wish to know at what angle θ from the horizontal will the berth come to equilibrium if we pull it out by a horizontal force F and what are the forces apply by the hinges (figure 8b).

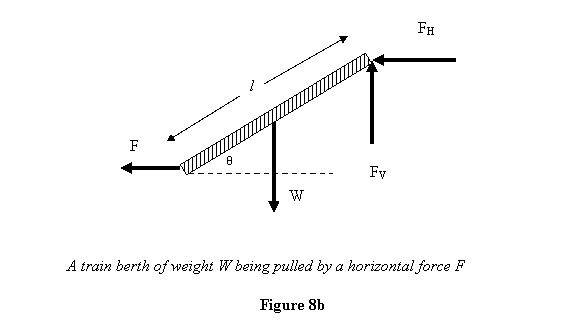
Let the weight of the berth be W and its width l. Let the forces applied by the hinges be F_H in the horizontal direction and F_V in the vertical direction. By equilibrium conditions

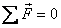
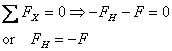
where the negative sign for F_H implies that it is in the direction opposite to that assumed.

Similarly

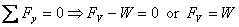
To find the angle we apply the moment or torque balance equation about the hinges. Weight W gives a counter clockwise torque of 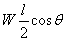and the force F gives a clockwise torque of Fl sin?

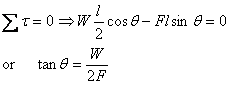
I should point put that if the hinge is not freely moving (for example due to friction) then it can produce a moment (couple) that will oppose any tendency to rotate and will have to be taken into account while considering the torque balance equation.

Next we look at a built in or fixed support as shown in the figure.

 

Let us analyze what happens in these cases when a load is applied. Let us look at the built-in support.

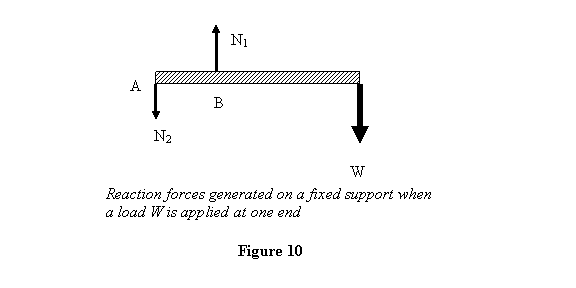
As the load is put on, the beam will tend to move down on the right side pushing the inner side up. This will generate reaction forces as shown schematically in figure 10. The generated forces can be replaced by a couple and a net force either about point A or B as follows (see figure 11). Add zero force N₁ -N₁ at point A then the original N₁ and -N₁ give a couple and no force and there is a net force ( N₁ -N₂) at A.

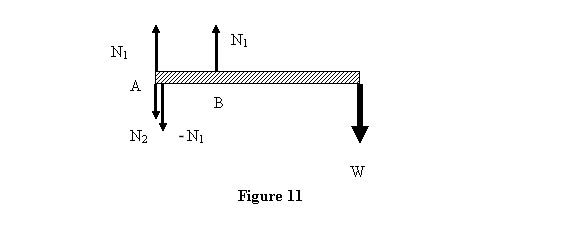
We could instead have added a zero force N₂ - N₂ at B and then would have obtained an equivalent system with a different couple moment than the previous case and a net force (N₁ - N₂) at B. I leave this for you to see. You may be wondering by now at which exactly does the force really act and what is the value of the couple. Actually in the present case the two unequal forces act on the beam so the torque provided by them is not independent of the point about which it is take. In such cases, as we will learn in the later lectures, the force effectively acts at the centroid of the force and the couple moment is equal to the torque evaluated about the centroid. In any case we can say that a built-in support provides a couple and a force. We give the schematic picture above only to motivate how the forces and the couple are generated. In reality the forces are going to be distributed over the entire portion of the support that is inside the wall and it is this distribution of force that provides a net force at the centroid and a couple equal to the torque calculated about the centroid, as we will see in later lectures. Note that deeper the support is fixed into a wall, larger would be the couple provided by it. Hence whereas to hang a light photo-frame or a painting on a wall a small nail would suffice, a longer nail would be better if the frame is heavy. In addition to providing a force perpendicular to the support and a couple, a fixed support also provides a force in the direction parallel to itself. Thus if you try to pull out the support or try to push it in, it does not move easily. 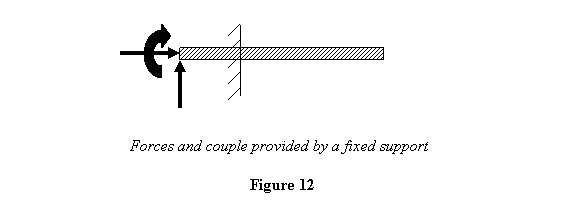The forces and couple provided by a fixed support are therefore as shown in figure 12.

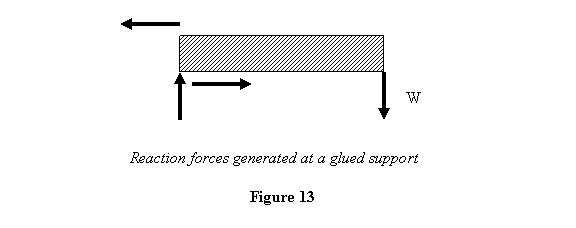
Let us now look at the support welded/ glued to the well. In that case suppose we put a load W at the end of the beam, you will see that the forces generated will be as shown below in figure 13.

where in this particular case the horizontal forces must be equal so as to satisfy

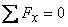
Thus the horizontal forces provide a couple and the beam can be said to provide a couple a force in the direction perpendicular to the support. Further a glued support also cannot be pulled out or pushed in. Therefore it too is capable of providing a horizontal nonzero reaction force. Thus a welded or glued support can also be represented as shown in figure 12. Note that wider the support, larger moment it is capable of providing. Let us now solve an example of this.

Example: You must have seen gates being supported on two supports (see figure 14). Suppose the weight of the gate is W and its width b. The supports are protruding out of the wall by a and the distance between them is h. If the weight of the gate is supported fully by the lower support, find the horizontal forces, vertical forces and the moment load on both the supports.

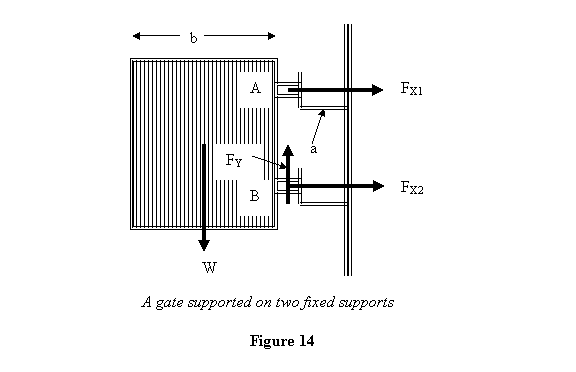
To solve this problem, let us first find out what are the forces required to keep the gate in balance. The forces applied by the supports on the gate are shown in figure 14. Since the weight of the gate is fully supported on the lower support all the vertical force is going to be provided by the lower support only. Thus

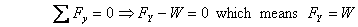
Similarly

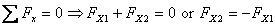
To find, 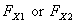, let us take moment about point A or B

Let us make 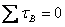. This gives (following the convention that counterclockwise torque is positive and clockwise torque is negative)

The negative sign for F_X2 means that the force's direction is opposite to what it was taken to be in figure 14. We also wish to find the forces and couple on the support. By Newton 's III^rd Law, forces on the support are opposite to those on the gate. Thus the forces on the two supports are:

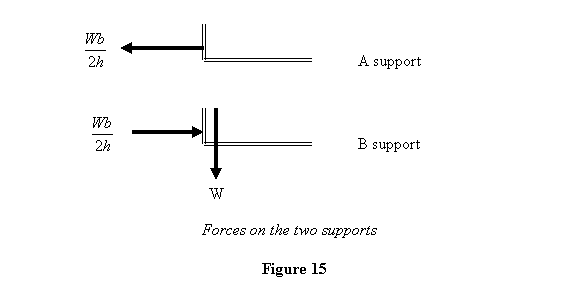
You see that support A is being pulled out whereas support B is being pushed in (we observe an effect of this at our houses all the time: the upper hinges holding a door tend to come out of the doorjamb). Now the force by the wall on support A will be 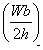to the right to keep it fixed in its place. On the other hand the situation for the lower support is more involved. The lower support will be kept in its place by the wall providing it horizontal and vertical forces and a torque. 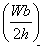The net horizontal force is to the left and the net vertical force is W pointing up. The lower support also balances a torque. Taking the torques about the point where it enters the wall, its value comes out to be

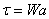
If we assume that the net vertical force and the torque is provided by only two reaction forces at two points as in figure 10, these two reaction forces can be calculated easily if we know the length of the portion inside the wall. I leave it as an exercise. In solving this, you will notice that the reaction forces are smaller if the support is deeper inside the wall. As pointed out earlier, in reality the force is going to be distributed over the entire portion of the support inside the wall. So a more realistic calculation is a little more involved.

To summarize this lecture, we have looked at some simple engineering elements and have outlined what kind of forces and torques are they capable of applying. In the next lecture we are going discuss forces in three dimensions. We are also going to look at conditions that forces with certain geometric relations should satisfy for providing equilibrium.