In the previous lecture we have defined
a couple moment. With this definition, we can now
represent a force 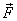 applied
on a body pivoted at a point as the sum of the same
force on it at the pivot and a couple acting on it.
This is shown in figure 1. Thus if the bar shown
in figure 1 is in equilibrium, the pivot must be
applying a force
applied
on a body pivoted at a point as the sum of the same
force on it at the pivot and a couple acting on it.
This is shown in figure 1. Thus if the bar shown
in figure 1 is in equilibrium, the pivot must be
applying a force 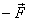 and
a counter couple moment on it.
and
a counter couple moment on it.
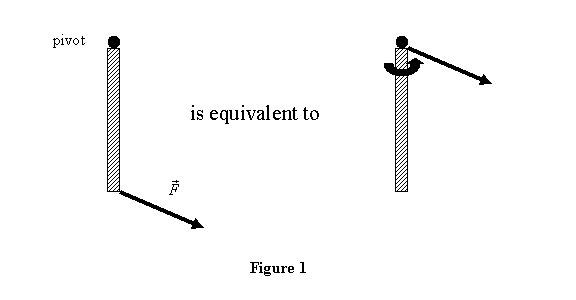
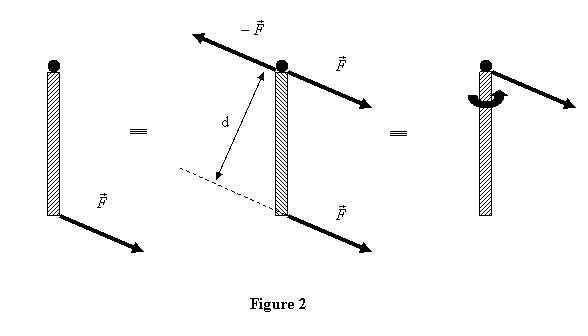
To
see the equivalence, let us take the example above
and add a zero force to the system at the pivot point.
This does not really change the force applied on
the system. However, the trick is to take this zero
force to be made up of forces  and
and 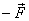 as
shown in figure 2. Now the original force
as
shown in figure 2. Now the original force 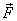 and
and 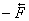 at
the pivot are separated by distance d and
therefore form a couple moment of magnitude Fd .
In addition there is a force
at
the pivot are separated by distance d and
therefore form a couple moment of magnitude Fd .
In addition there is a force 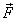 on
the body at the pivot point. The combination is therefore
a force
on
the body at the pivot point. The combination is therefore
a force 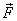 at
the pivot point P and a couple moment
at
the pivot point P and a couple moment 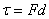 .
Notice that I am not saying
.
Notice that I am not saying 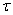 about
the pivot. This is because a couple is a free vector
and its effect is the same no matter at which point
it is specified.
about
the pivot. This is because a couple is a free vector
and its effect is the same no matter at which point
it is specified.
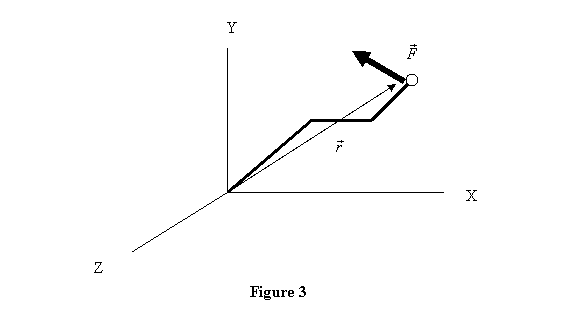
Example: You must
have seen the gear shift handle in old buses. It
is of Zigzag shape. Let it be of the shape shown
in figure 3: 60cm at an angle of 45° from the
x-axis, 30cm parallel to x-axis and then 30cm again
at 45° from the x-axis, all in the x-y plane
shown in figure 3. To change gear a driver applies
a force of 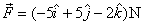 on
the head of the handle. We want to know what is the
equivalent force and moment at the bottom i.e., at
the origin of the handle.
on
the head of the handle. We want to know what is the
equivalent force and moment at the bottom i.e., at
the origin of the handle.
For this again we can apply a zero
force i.e., ( 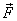 and
and 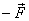 )
at the bottom so that original force and
)
at the bottom so that original force and 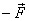 give
a couple moment
give
a couple moment
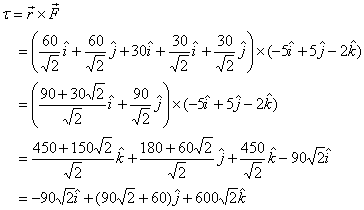
Thus equivalent force system is a
force 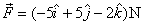 at
the bottom and a couple equal to
at
the bottom and a couple equal to 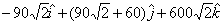 Nm.
Nm.
Having obtained equivalent force systems, next we
wish to discuss what kind of forces and moments do
different elements used in engineering mechanics
apply on other elements.