Lecture 26
Harmonic oscillator III: Forced oscillations

In the previous two lectures, you have learnt about free harmonic oscillator and damped harmonic oscillator. In this lecture we study what happens when a harmonic oscillator is subjected to a force. The simplest case is when an oscillator is subjected to a constant force F . In that case nothing much takes place except that the equilibrium point gets shifted by (F/k). You see an example of it when a mass is attached to a vertical spring. Mathematically we write

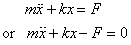
This can be written as

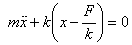
for an undamped oscillator and

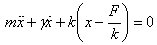
for a damped oscillator. Define a new variable 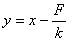  so that the equation reads (I write only the undamped oscillator equation)

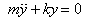
This is the equation you are well familiar with. From its solution, that for x is written as

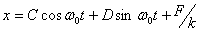
So the mass oscillates about 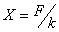. I now take up an oscillator subjected to a time-dependent force.

A general time-dependent force F(t) can always be decomposed into its Fourier components like 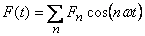so generally we study an oscillator subjected to a force of the form. 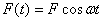, where 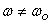and F is the amplitude of the force. Let me start by first studying the motion of an undamped oscillator under such a force.

The equation of motion for an undamped oscillator under a time-periodic force is

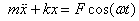
or equivalently

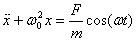
The general solution is a combination of homogeneous part of the equation and a particular solution x_p. Thus

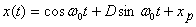
Here you can check that

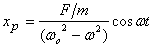
Let me start the oscillator from rest at equilibrium. It starts moving because of the applied force. The initial conditions then are 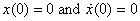. Under these conditions the solution comes out to be

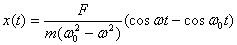
So the general solution is a combination of motion of two frequencies. The resulting motion can be represented on a phasor diagram by adding the two motions vectorially. This shown at t = 0 and two other different times in figure 1.

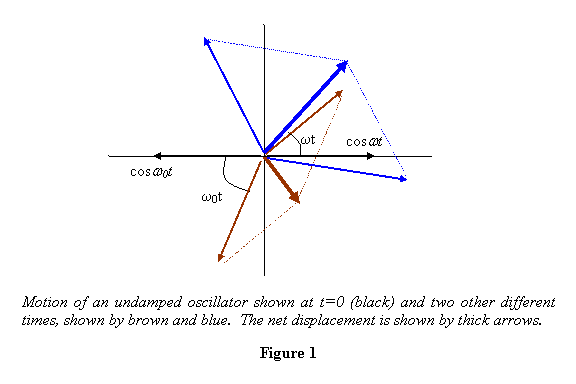
As is clear from the figure, at t = 0, the net displacement is zero. As the time progresses, the displacement changes with the length of the rotating vector also changing with time. As an illustrative example, I take the frequency 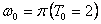, and two different frequencies, 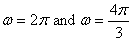for the force. The resulting solutions are shown in figure 2.

 

 

 

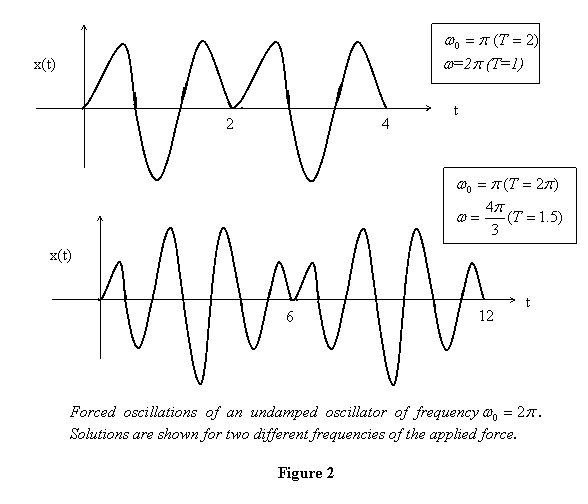
So you see from the figure above that the maximum displacement of oscillations keeps changing. This is what I had inferred from the phasor diagram also. The motion is still periodic and reminds us of the phenomena of beats.

Interesting is the case when 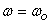. However, I cannot put it directly in the formula become we are dividing by 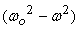. So we have to take the limit 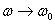. Let me substitute in the formula 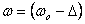or 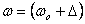and take 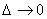. This leads to

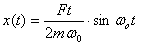
Thus the displacement keeps on increasing with time oscillating with the frequency of the oscillator. This is the phenomena of resonance. The corresponding plot of displacement is shown in figure 3.

 

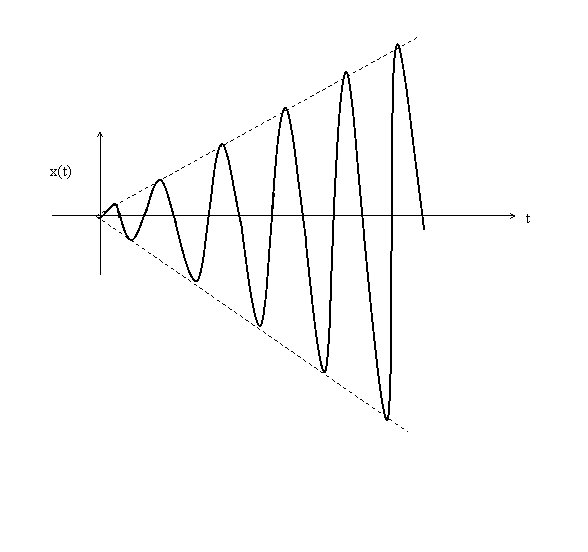
Forced oscillations of an undamped at resonance

Figure 3

Having discussed forced oscillations for undamped oscillator, we now move on to study a damped oscillator moving under the influence of a periodic force. The equation of motion then is

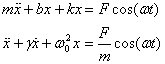
As earlier, the general solution of this equation is going to the sum of the homogenous and inhomogeneous part. So

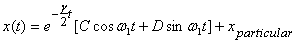
As the time progresses 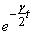will make the homogeneous solution die down so finally the only solution remaining will be

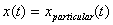
This is known as the steady state solution. Obviously it does not depend on the initial conditions. Let us now find this solution.

For the equation of motion

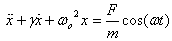
I assume a steady state solution of the form 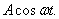  But when substituted in the equation, this will give rise to a term containing 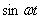because of 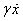in the equation. So a general solution should be of the form.

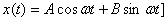
When substituted in the equation, this leads to

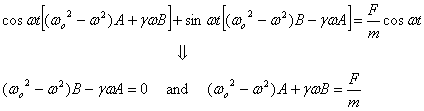
These equations give

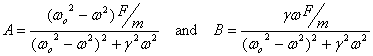
So the general solution is

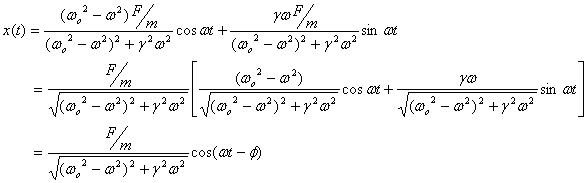
where

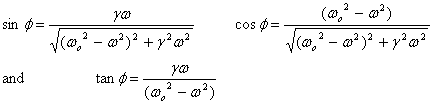
Thus after reaching steady state, the displacement lags behind the applied force by an angle 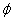with 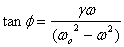  and oscillates with an amplitude

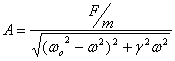
The oscillation frequency of steady-state solutions is obviously equal to the frequency of the applied force. A typical displacement and its shift with respect to the applied force are shown in figure 4.

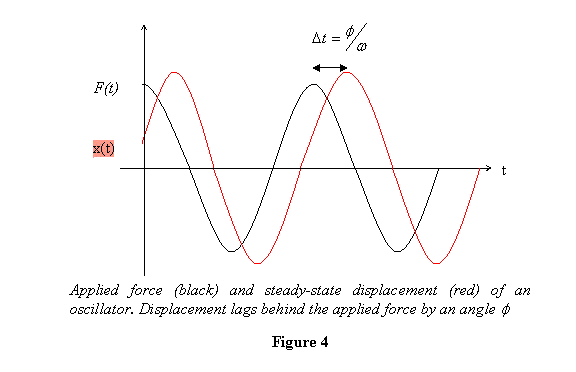
As far as getting the steady state solution for a forced damped oscillator is concerned, we are done. What we need to do now is to analyze the solution in different situations.

First of all we notice that irrespective of whether the system is lightly damped or heavily damped, it will always oscillate under an applied time-periodic force. Let us first consider the case of light damping and see how the amplitude varies with the applied frequency. The amplitude as a function of ω is given as

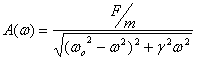
This amplitude goes to 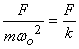as 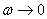. This is nothing but the stretch of the spring under a constant force. For very large frequencies 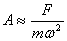. In between the amplitude has a maximum at 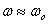as is easily seen. So in this case, the amplitude as a function of frequency looks as shown in figure 5 for two different values of γ .

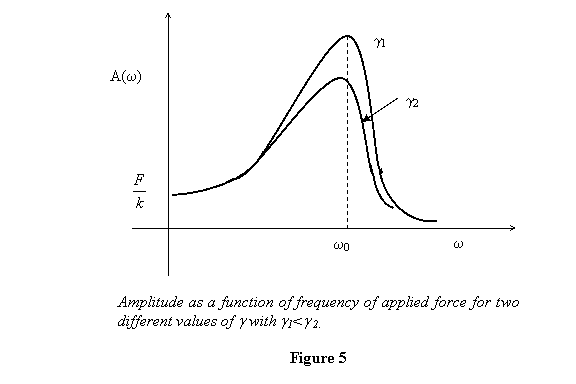
It is clear from the figure that the amplitude is maximum around 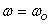which reminds us of the phenomenon of resonance for undamped oscillator. For large γ values the peak shifts to the left (lower frequency).

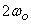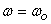For heavy damping ( γ > ) we do not see any amplitude maximum near but the system has large amplitude for low frequencies. A schematic plot of amplitude as a function of frequency looks like figure 6. It is evident that only for low frequencies the system oscillates with reasonable amplitude.

What about the phase of the system with respect to the applied force? I leave this as an exercise for you to plot the phase of displacement as a function of frequency.