Next I discuss how much power is absorbed by the system to maintain its oscillations.

Power absorption in a forced damped oscillator : Since a damped system has a retardation force opposing its motion, it dissipates energy. For it to maintain a steady-state the applied force constantly supplies energy to it. It is this power that I now calculate. Power given to the system is 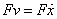since I am considering a one dimensional system. Otherwise I would have taken the dot product between the force and the velocity. The calculation proceeds as follows

 

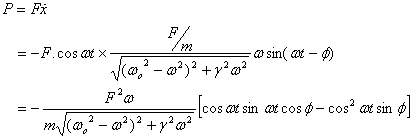
Since the average of 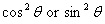over a cycle is ½ and that of 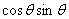zero, the average the last expression with respect to time over one cycle gives

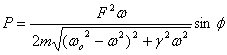
This is the average power being supplied to the system to maintain its steady-state. The same can also be obtained by realizing that in steady-state the power given to the system is the same as power dissipated by it. Power dissipated is the drag force 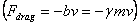times the velocity. This is therefore calculated as follows:

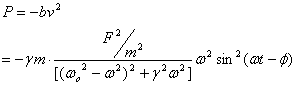
Taking its time average over a cycle then gives the average dissipated power

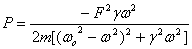
which is the same result as obtained above. The negative sign shows that this is the energy lost, and produced heat due to the friction in the system. Since the amplitude of the motion is largest when the force has a frequency close to the natural frequency of a system, it is expected that the power loss will also be maximum near that frequency. I have plotted the power dissipated in a forced damped harmonic oscillator in figure 7.

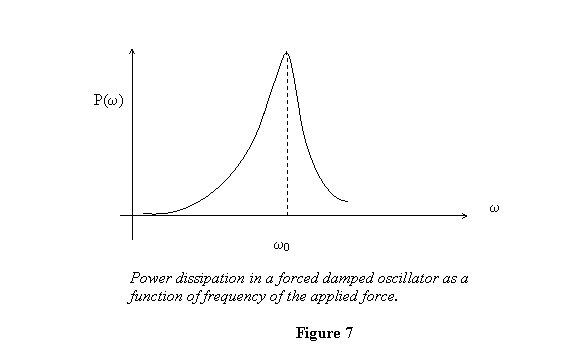
The curve peaks at ω₀ so the power absorption is indeed maximum at the resonance frequency.

Finally I relate the Q factor of a damped oscillator with the power versus frequency curve given above. To do this let us see at what frequency does the power absorption is ½ of its peak value. The calculation, in which we make the frequency-dependent factor in the expression for power dimensionless and equate it to ½, is given below

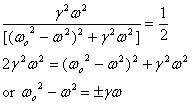
Solving this equation for the frequency ω under the approximation of light-damping gives

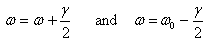
The frequency width from 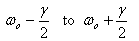is known as full width at half maximum (FWHM) and its value is γ. Thus the quality factor can also be interpreted as

 

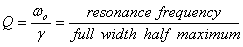
This pretty much sums up what I want to tell you about forced oscillations. I want to point out that we have focused here strictly on the steady-state solutions for the damped oscillator. However, before steady-state is reached, the system goes through transient motion, which is also important to understand in designing of systems.

 

This lecture brings us to the close of our discussion on harmonic oscillators.