To summarize, I have covered three cases for the heavy damping situation and got

(i) Spring stretched and block released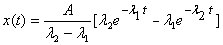

(ii) The block given an initial positive velocity at equilibrium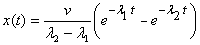

(iii) Spring stretched out and the block given a velocity in the negative direction

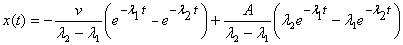
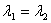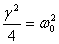I would now like to tell you about the case when . This is known as the critically damped case. Obviously this situation arises when . I can easily find solutions for such case if I take the limit 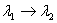in the cases of heavy damping just studied. Please note that I cannot straightaway take 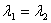in the expressions above because I am dividing by 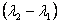. Taking the limit gives for the three cases studied above

(i)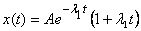
(ii)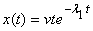
(iii)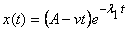

As remarked above, the cases we have just discussed correspond to critical damping. In this situation 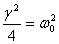and 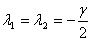. Mathematically, in this case there is only one solution  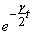   ( )   that we get from the equation for λ because of its double root. The other solution is found to be 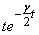. That is precisely what we have found by taking appropriate limit.

Critically damped system and used when we want a system to return to its equilibrium position after receiving an impulse, although one is tempted to say that use a heavily damped system for this purpose. I would like you to understand this by carrying out the following exercise.

 

Exercise : The block on a damped spring-mass system is given an initial velocity v from equilibrium. Given a damping coefficient γ, plot the distance versus time graph for the critically and heavily damped cases. For ease of calculation take the heavy damping to be very large so that 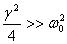and make appropriate approximations.

 

Having discussed the heavily and critically damped systems, we move on to lightly damped system. In such systems 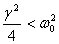  so that

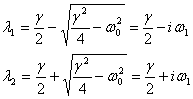
So the general solution is

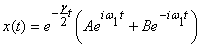
Or equivalently

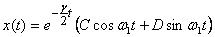
In case when 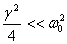, it is called very light damping and in such case .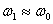

Let us now take a particular can when the block is stretched to distance A and is released from rest. I leave the details of the solution to be worked out by you. Here I give the final answer which is

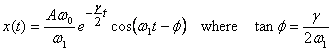
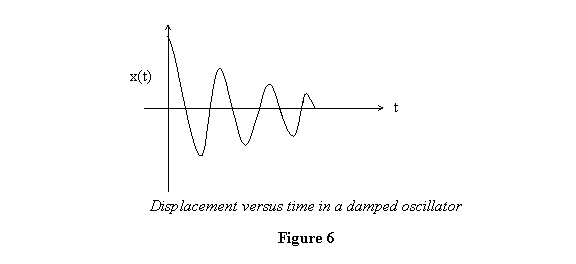
This solution is plotted schematically in figure 6. Notice how the maximum distance reached by the block decreases with time.

When we consider light damping, generally we are dealing with cases where we want the decay to be small. Thus within the time that the motion decays, there are many-many oscillations. Thus we can then write the displacement as

because 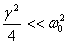implies that 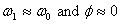. The equation above is interpreted as the oscillation taking place with frequency w 0 with time-dependent amplitude 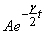. Mathematically what this means is that 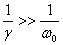  so there are two time scales in the problem. Let me now talk about the energy of the system. Since the amplitude is decreasing with time, the system is obviously losing energy. I want to calculate the rate of energy loss in the system. First, there and many oscillations over the time interval of 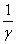, which is also a very large time span. Further, the decay of the amplitude is very small over a few periods. This allows us to talk in terms of the average energy of the system. What it means is the energy averaged over a few cycles around a given instant. I now calculate it.

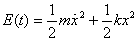
Now use 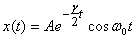to calculate this energy. It gives

Now taking an average over a few cycles under the approximation that the exponentially decaying term be treated as roughly a constant over these cycles and neglecting the term proportional to γ² , I get

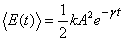
where angular brackets denote the average energy. So the average energy decays exponentially for a lightly damped oscillator.

I now define the quality factor or Q for an oscillator. As mentioned earlier, we are interested in systems where 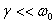; it is in such cases only that talking about Q makes sense. Q is defined as

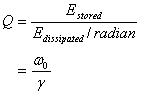
High Q value for an oscillator means that there is very low leakage compared to the store energy.

Finally I summarize the lecture by telling you that we have covered the cases of heavy, critical and light damping in this lecture. You must have noticed that I have made a lot of graphs in this and the previous lecture. Please do that when you solve a problem. It will give you a feel for the system.