In the previous lecture, I covered some basic aspects
of simple harmonic oscillations. We considered the
equation
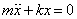
and saw how its motion is described. A general solution
of this equation is
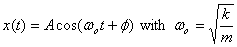
I now make the system little more realistic and introduce
damping into the system. Let us first look at what
happens if we introduce friction into the system.
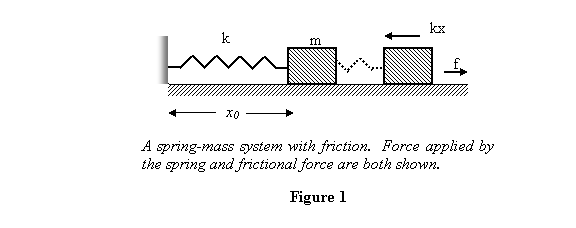
I consider again our prototype spring-mass system
and let there be a constant frictional force f on
the mass. This force will always oppose the motion
so the system will eventually come to a stop. Let
us see when does it do that?
The simplest way of seeing when he system will stop
is the through the consideration of energy. But I
would like to solve the problem by employing the
equation of motion. I will later solve it from energy
considerations also. Here is one case where I will
have to analyze motion step by step because as the
velocity direction changes, so does the force direction.
So let us pull the spring out to a distance A and
let it move towards the equilibrium point (see figure
1).
When the block is moving towards the left, equation
governing its motion will be
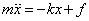
In the above, the frictional force f sign
is positive because the mass is moving in the negative x direction
and therefore the frictional force is in positive x direction.
This equation can be recast into the form
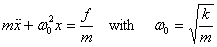
We have encountered such kind of equation earlier.
It has a homogeneous part 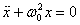 and
an inhomogeneous term on the right-hand side. So
the general solution is
and
an inhomogeneous term on the right-hand side. So
the general solution is
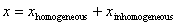
where

Thus
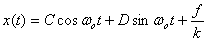
With the initial conditions 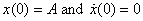 ,
the solution is
,
the solution is

This is the solution when the block is moving to the
left. Since
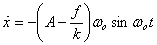
so the block will come to a stop when 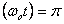 .
At that time
.
At that time
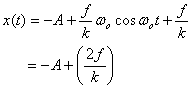
So by the time the block comes to a stop it has lost 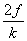 distance
from its amplitude. And this loss is irrespective
of the distance from where the block starts its motion
from. This should then also happen when the block
starts coming back. Let us find that out. On its
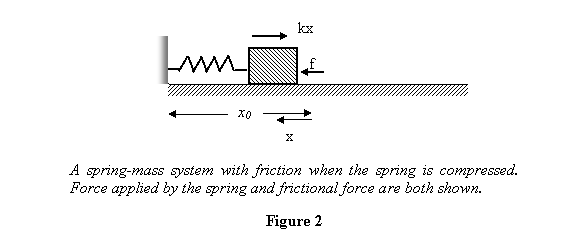
way back (see figure 2), the block follows the equation
distance
from its amplitude. And this loss is irrespective
of the distance from where the block starts its motion
from. This should then also happen when the block
starts coming back. Let us find that out. On its
way back (see figure 2), the block follows the equation
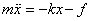
Notice that the sign of the friction force is now
negative. This is because now the block is traveling
to the right and therefore the friction force acts
towards the left (see figure 2).
Now we have to solve this equation with the initial
condition that
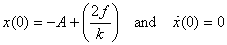
I leave it as an exercise for you to get the solution.
It is
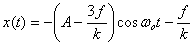
The corresponding velocity is proportional to ω0t,
and therefore goes to zero again after a time interval
of 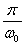 .
At that time
.
At that time 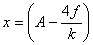 .
Thus every half time the block goes from one
extreme to the other, it loses a distance of
.
Thus every half time the block goes from one
extreme to the other, it loses a distance of 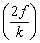 ,
and in each cycle it loses a distance of
,
and in each cycle it loses a distance of 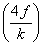 .
Question is how many cycles does the block complete
before it comes to a stop. The block stops when
its final displacement is
.
Question is how many cycles does the block complete
before it comes to a stop. The block stops when
its final displacement is 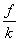 .
If it completes n cycles before that,
we have
.
If it completes n cycles before that,
we have
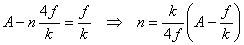
The same result can also be obtained, as I said earlier,
by energy methods. If stretched by A the
total energy of the system is 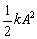 .
Let us say that before stopping, the block it compresses
the spring by A1. Then its energy
will be
.
Let us say that before stopping, the block it compresses
the spring by A1. Then its energy
will be 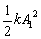 .
The loss in the energy is caused by friction. Thus
.
The loss in the energy is caused by friction. Thus
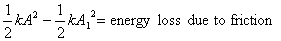
The total distance moved by the block is (A+A1) and
so the energy lost against friction is f(A+A1) .
Thus the equation transforms to
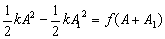
and gives
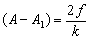
which is the same loss in amplitude over half a cycle
as obtained earlier. The rest of the analysis is
the same as done earlier.
Having dealt with the constant friction case, we now
consider the most common example of damped oscillations.
This is the oscillator where damping force is proportional
to the velocity i.e.,
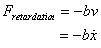
In this case, the equation of motion is
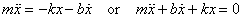
Writing 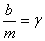 we
get
we
get
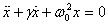
This is the equation for a damped oscillator. The
equation is homogeneous in x so we assume
a solution 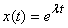 and
substitute it in the equation to get.
and
substitute it in the equation to get.
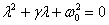
which gives
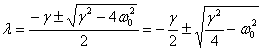
So the general solutions are
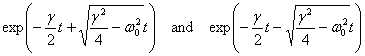

Except in the case when 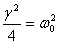 (we
will deal with it later) the behavior of the solution
depends on the relation magnitude of γ and ω0.
Let us first consider the case when
(we
will deal with it later) the behavior of the solution
depends on the relation magnitude of γ and ω0.
Let us first consider the case when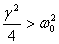 .
In that case
.
In that case
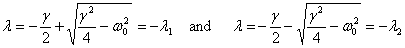
The general solution then is
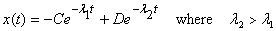
This is known as a heavily damped oscillator. The
coefficients C and D depend on
the initial conditions. For example if I stretch
the spring to a distance A and release the
block, let us see what happen in this case. By initial
conditions
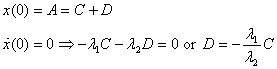
This leads to
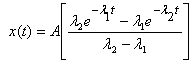
A t → ∞ this
solution behaves like 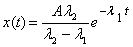 .
The general solution is displayed in figure 3.
.
The general solution is displayed in figure 3.
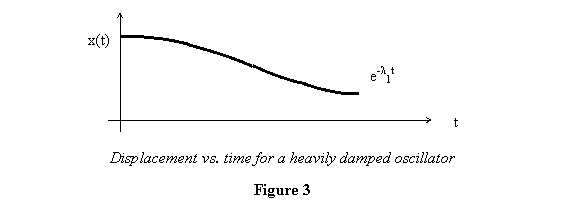
It is clear from the figure that there are no oscillations
in this case the block slowly comes to rest at x
= 0 ,
i.e. the equilibrium point. I now explore another
situation. Suppose we give an implies (speed v )
at t = 0 then the boundary conditions are
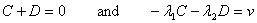
Thus the solution would be
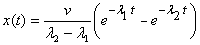
In this case the distance versus time graph looks
as shown in figure 4.

The
figure clearly shows that the block goes out to a
maximum distance and then comes back and stops at
the equilibrium point. So in both the cases studied
above the mass does not cross the equilibrium point.
Next I ask: what if we stretch the mass out to a
distance A and give it an initial impulse
from that point (in negative direction). Then the
initial conditions will b

Solution in this case comes out to be
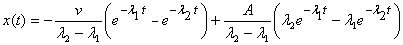
The solution is plotted schematically in figure 5.

It is clear that in this case the particle moves towards
the equilibrium point, crosses it, goes a distance
and comes back. However on its way back it slowly
comes to rest at the equilibrium point and does not
cross it. So in heavy damping cases, the block passes
the equilibrium point at most once and its distance
decays exponentially as 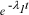 .
.