The
general equation governing rotation of a rigid body:
Having
dealt with situations where components of 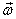 are
constant, we now ask what happens when are
constant, we now ask what happens when 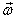 is
also changed. For this let me look at the expression
for the angular momentum in the principal axis frame
again. It is is
also changed. For this let me look at the expression
for the angular momentum in the principal axis frame
again. It is
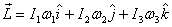
I now give a slightly different derivation for the rate
of change of 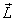 .
In doing this derivation I keep in mind that as a rigid
body rotates, the unit vectors along its principal axes
also rotate and their rate of change is (see previous
lecture) .
In doing this derivation I keep in mind that as a rigid
body rotates, the unit vectors along its principal axes
also rotate and their rate of change is (see previous
lecture)
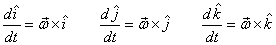
Now I differentiate 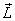 to
get to
get

Here the first term is due to the change in the components
of 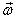 along
the principal axis and the second term is the
change in along
the principal axis and the second term is the
change in 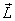 due
to its rotation. Notice that we recover the formula
derived earlier if the components of due
to its rotation. Notice that we recover the formula
derived earlier if the components of 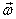 do
not change with time, i.e. do
not change with time, i.e. 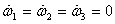 .
Let me repeat the interpretation of the equation:
at any instant we take the body rotating in the
principal axes frame at that time, i.e. the frame
is frozen at its position at that time and the
body is taken to be rotating in it. To see this
geometrically, let me take a two-dimensional
case. Shown in figure 10 are the principal axes
1 and 2 of a rigid body at times t and (t+ Δt) .
In time interval Δt the
body and the frame attached to it rotate by an
angle .
Let me repeat the interpretation of the equation:
at any instant we take the body rotating in the
principal axes frame at that time, i.e. the frame
is frozen at its position at that time and the
body is taken to be rotating in it. To see this
geometrically, let me take a two-dimensional
case. Shown in figure 10 are the principal axes
1 and 2 of a rigid body at times t and (t+ Δt) .
In time interval Δt the
body and the frame attached to it rotate by an
angle 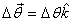 ,
and ω1 and ω2 change
to ω1 + Δω1 and ω2 + Δω2 .
With these changes let me calculate changes in
the components L1 and L2 in
the frame frozen at time t . ,
and ω1 and ω2 change
to ω1 + Δω1 and ω2 + Δω2 .
With these changes let me calculate changes in
the components L1 and L2 in
the frame frozen at time t .
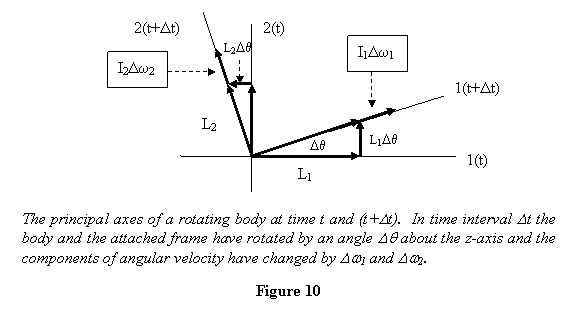
Looking at the figure, where I have shown all the changes
that have taken place during the time interval Δt , we get in the frame at time t
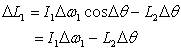
and
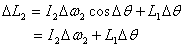
So the total change in the angular momentum is
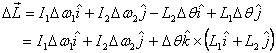
Dividing both sides by Δt and taking proper
limit gives
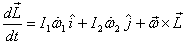
This gives you some idea about where this equation comes
from. Of course in a more accurate treatment, rotations
about the other axes also have to be taken into account.
For infinitesimal rotations, they can all be added up
and give the general equation
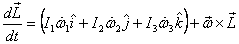
This gives
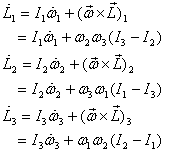
Each one of these rates of change should be equal to the
component of the torque in that direction .Thus
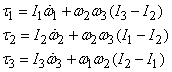
These are the most general equations governing the dynamics
of a rigid body and are known as Euler's equations. I
now use it to explain the third experiment I had suggested
in the beginning of Lecture 21.
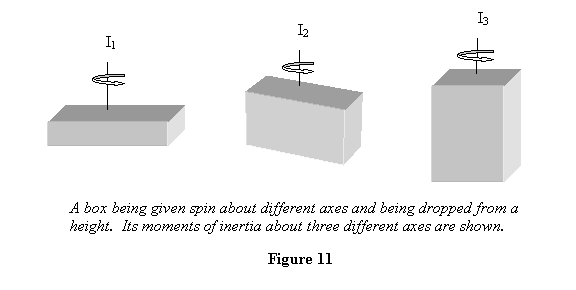
Example 4: Hold a rectangular box
at a height with one of its faces perpendicular to
the vertical, give it a spin and let it drop (see
figure 11). Describe its subsequent rotational motion.
This is an example of torque-free (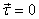 )
motion because there is no torque on the box
about its centre of mass. Thus its rotational motion
is governed by the equations )
motion because there is no torque on the box
about its centre of mass. Thus its rotational motion
is governed by the equations
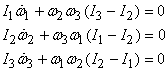
For a box similar to the one shown in figure 11 we
would generally have I3 > I2 > I1
.
Let me first consider the case when the box is given
a spin about its principal axis 1. Let me also assume
that in the process I also disturb it and give it
very small angular velocities ω2 and ω3 about
its axes 2 and 3, respectively. Since both ω2 and ω3 are very small, their product is second-order
in smallness and will be ignored. The Euler equations
and there are then as given below.
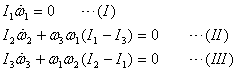
The first equation implies that ω1 is
a constant. Let me call it the spin rate ω0 .
Using this fact the other two equations are dealt
with as follows. Differentiate equation (II) with
respect to time to get
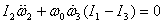
and substitute for 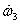 from
equation (III) to obtain from
equation (III) to obtain
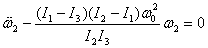
Since I3 > I2 > I1 , the equation above is of
the form
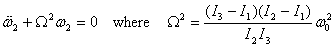
Its solution is of the form
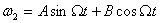
One can similarly get equation for ω3 also
and see that it also has similar oscillatory
solution. This implies that as the box falls down
it spins about axis 1 and oscillates about axes 2
and 3. Since magnitudes of ω2 and ω3 are
small, you see the box fall essentially spinning
only. The same thing will happen if we give initial
spin about axis 3. However something different happens
when the initial spin is about axis 2. Assuming ω1 and ω3 to
be small, in this case the Euler equations take
the following form right after the release of the
box.
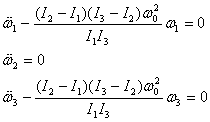
The second equation above implies that ω2 is
a constant and with I3 > I2 > I1 , the
other two equations take the form
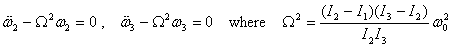
Solution of these equations is of the form
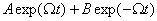
which indicates that right after the release, the angular
velocities about axes 1 and 3 will grow very fast and
take on a large value. Thus the box will start rotating
about all three axes and that is what you observe. Thus
we see that a rigid body is stable when it is given a
spin about the axes having the smallest or the largest
moment of inertia. However, if given a spin about the
axis with intermediate moment of inertia, it will be
unstable. Next I take up the case of precessing top that
I had not solved by employing Euler's equations earlier.
This is an example where a torque is also being applied
on the system
Example 5: Apply Euler's equations
to a precessing top and get its precession frequency Ω.
The top has a mass m and is spinning
at a rate of ωS (see
figure 12). Its centre of gravity is at a distance l from
the pivot point.
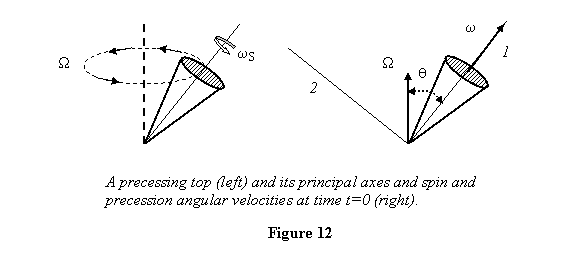
I have already discussed about the principal axes
of the top in example 2 above. With 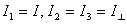 the
Euler's equations for the top are the
Euler's equations for the top are
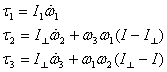
Now in applying Euler's equations you have to keep
in mind that the top is spinning. As such its principle
axes 2 and 3 also rotate about axis 1 with angular
frequency ωS . So the components
of angular frequency and torque in the direction
of these axes also change with time. Taking time
at which the position of the top is shown in figure
12 to be t = 0, I draw in figure 13
the position of axes 2 and 3 at time t .
In this figure, I have neglected the angle W
t through which the top and therefore the torque
vector itself has rotated. In other words I have
assumed that 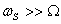 .
Thus the angular velocity and torque are shown
where they were at t = 0 . .
Thus the angular velocity and torque are shown
where they were at t = 0 .
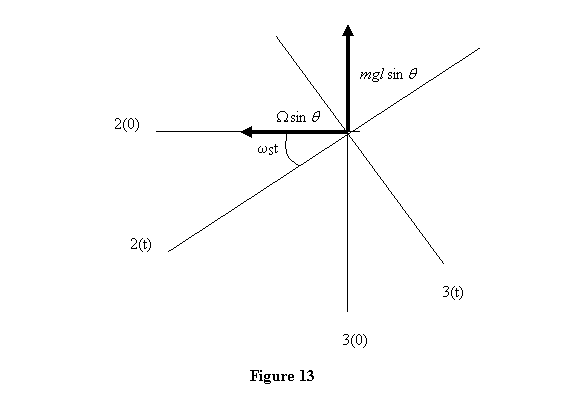
Looking at figure 13, it is clear that the components
of the angular velocity and the torque are

Substituting these in the Euler's equation for the top
gives
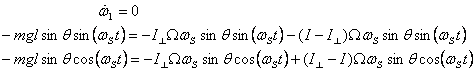
The first of these equations gives ω1 =
constant = ωS.
The other two equations give the same answer
which is
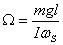
This is the answer that we have seen earlier. In solving
the Euler's equations for the top, we made the
assumption of 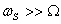 .
Further we assumed that the top only precesses
about the vertical. However, there is no reason why
it cannot posses a horizontal angular velocity ΩH also.
Assuming the existence of Ω and ΩH and
then solving the Euler's equations will give
a more complete solution for the motion of a
spinning top. It in fact gives the nutating motion
also. You may want to try getting this general
solution. .
Further we assumed that the top only precesses
about the vertical. However, there is no reason why
it cannot posses a horizontal angular velocity ΩH also.
Assuming the existence of Ω and ΩH and
then solving the Euler's equations will give
a more complete solution for the motion of a
spinning top. It in fact gives the nutating motion
also. You may want to try getting this general
solution.
With this lecture I end of the topic of rigid-body rotation.
|