Having analyzed the motion of particles in different
situations, let us now focus on a very special kind
of motion: that of oscillations. This is a very general
kind of motion seen around you: A partial moving
around the bottom of a cup, a pendulum swinging,
a clamped rod vibrating about its equilibrium position
or a string vibrating. A good first approximation
to these motions is the simple harmonic oscillation.
Let us see what does that mean? At a stable equilibrium
point, the force on a body is zero; not only that,
as a particle moves away from equilibrium, its potential
energy increases and it is pulled back towards the
equilibrium point. Thus around a stable equilibrium
point x0 (for simplicity, let me take
one-dimensional motion) the potential energy 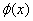 can
be written as
can
be written as
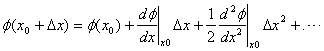
Since at an equilibrium point, the force F(x0
) on the particle vanishes,
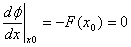
Further, because Φ(x) has a minimum at x0 , this gives
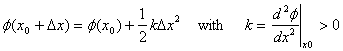
Writing 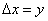 I
get
I
get
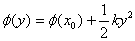
and the corresponding equation of motion for a mass m as
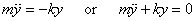
As I will show a little later, the solution of this
equation is of the form
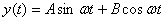
and is known as the simple harmonic motion. It is
the simplest possible motion about a stable equilibrium
point. Of course if k = 0 , the force will
have higher order dependence on y and the
motion becomes more complicated. Further, even if 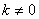 ,
if we include higher order terms, the resulting motion
will become more complex. It is for this reason that
we call the motion above simple harmonic motion.
We will see that this itself is quite a rich system.
A system that performs simple harmonic motion is
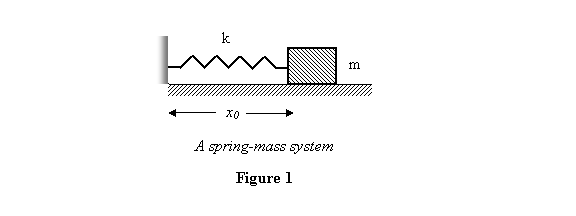
called a simple harmonic oscillator. A prototype
if this system is the spring-mass system with k being
the spring constant and m the mass of the
block on the spring (figure 1).
,
if we include higher order terms, the resulting motion
will become more complex. It is for this reason that
we call the motion above simple harmonic motion.
We will see that this itself is quite a rich system.
A system that performs simple harmonic motion is
called a simple harmonic oscillator. A prototype
if this system is the spring-mass system with k being
the spring constant and m the mass of the
block on the spring (figure 1).
In these lectures, I will talk about the motion of
this system and how it is represented by a phasor
diagram. I will then introduce damping into the system.
The simplest damping is a constant opposing force
like friction and next level is a damping proportional
to the velocity. Then I will apply a force on the
system and see the motion of force damped and undamped
oscillator. Along the way, I will solve many examples
to show wide applicability of simple harmonic motion.
To start with let us take our prototype system of
mass and spring with unstretched length of the spring  so
that equilibrium distance of the mass is
so
that equilibrium distance of the mass is 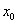 .
Now when the mass is displaced about
.
Now when the mass is displaced about 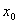 by x in
the positive direction, the force is in negative
direction so that
by x in
the positive direction, the force is in negative
direction so that
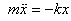
or

This is the general equation for simple harmonic oscillator.
Recall that in such cases we assume a solution of
the form
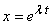
and substitute it in the equation to get
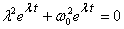
Since this equation is true for all times, we should
have
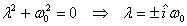
Thus there are two solution 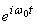 and
and 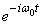 .
A general solution is then given in terms of a linear
combination of the two solutions so let us write
.
A general solution is then given in terms of a linear
combination of the two solutions so let us write
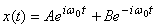
Since 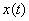 is
real it is clear that
is
real it is clear that 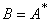 .
Thus
.
Thus
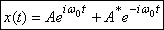
If we take A = AR + iAI ,
where both AR and AI are
real then the solution above takes the form
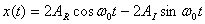
which alternatively can be written as
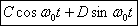
Another equivalent way of writing the solution is
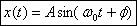 or
or 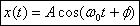
where

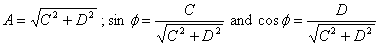
A is the maximum distance that the mass travels during
a simple harmonic oscillation. It is known as the
amplitude of oscillation. The quantity 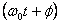 is
known as the phase with Φ being the initial
phase. All the boxed equations above are equivalent
ways of writing the solution for a harmonic oscillator.
The general graph depicting the solution
is
known as the phase with Φ being the initial
phase. All the boxed equations above are equivalent
ways of writing the solution for a harmonic oscillator.
The general graph depicting the solution 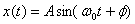 is
given in figure 2.
is
given in figure 2.
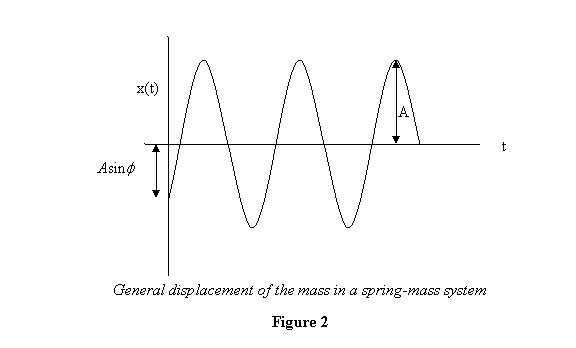
Thus A is the maximum distance traveled
by the block and 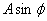 gives
its initial displacement. The constants C and D or A and
gives
its initial displacement. The constants C and D or A and 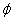 are
determined by the initial conditions, i.e. initial
displacement and velocity of the mass. In general
any two conditions are enough to determine the constants.
are
determined by the initial conditions, i.e. initial
displacement and velocity of the mass. In general
any two conditions are enough to determine the constants.
For a displacement
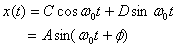
the velocity of the mass is given by
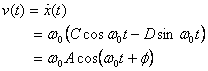
Thus the maximum possible magnitude of the velocity
is ω0 A . The general displacement and
the corresponding velocity of the mass with respect
to time are displayed in figure 3.
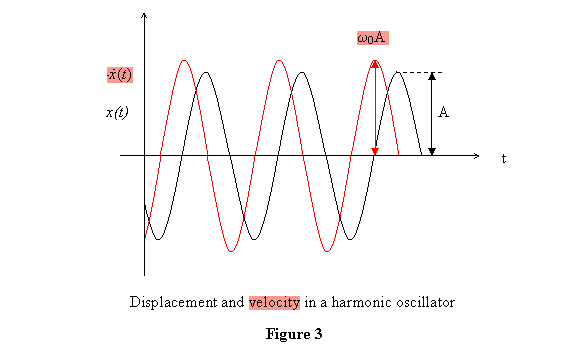
It is clear from the figure that for a given displacement,
the velocity is such that when displacement is at
its maximum or minimum, the velocity is zero and
when the displacement is zero, the velocity has the
largest magnitude. This is physically clear. When
the spring is compressed or stretched to its maximum,
the particle is at rest and when the particle passes
through the equilibrium point, its speed is at its
maximum. Let me now solve a few examples.