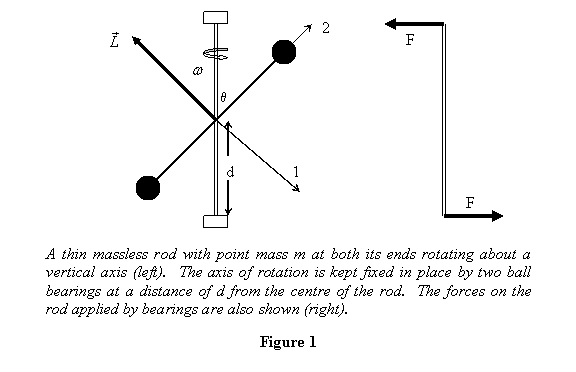
Example
1: A thin massless rod of length 2l has
a point mass m at both its ends. It is
rotating with angular speed w about a vertical axis
passing through its centre and at an angle θ from
it, as shown in figure 1. If the axis of rotation
is held at its two ends by ball bearings, calculate
the force that the ball bearings apply on the axis.
The ball bearings are placed symmetrically from the
centre of the rod at a distance d each.
Recall from the previous lecture that I had taken
the principal axes (1,2,3 ) with (1,2)
as shown in figure 1 and axis 3 perpendicular
to them. The moments of inertia about the principal
axes are
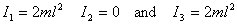
The angular velocity and the angular momentum of the rod-mass
system are
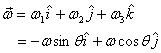
and
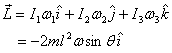
All the parameters - mass m , length l and
angle θ - in the equation above are constant
so the magnitude of the angular momentum is also a constant.
As such we can apply the formulae given above to get
the components of the torque to be applied as
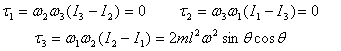
Thus the torque needed to keep the rotating rod in its
position is in the direction of principal axis 3 of the
body. As was noted above, the torque is indeed perpendicular
to 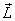 .
The torque is provided by the forces applied by the bearings.
When the rod is in the plane of the paper, as shown in
the figure, the force would be to the left at the upper
end and to the right at the lower end of the rod (see
figure 1). And their magnitudes will be equal since the
CM of the rod has zero acceleration. Thus the forces
provide a couple equal to .
The torque is provided by the forces applied by the bearings.
When the rod is in the plane of the paper, as shown in
the figure, the force would be to the left at the upper
end and to the right at the lower end of the rod (see
figure 1). And their magnitudes will be equal since the
CM of the rod has zero acceleration. Thus the forces
provide a couple equal to 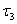 .
Their magnitude is .
Their magnitude is
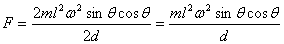
There is another method of calculating 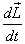 that
we describe now. that
we describe now. 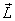 has
one component has
one component 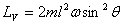 in
the direction of in
the direction of 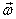 and
the other component and
the other component 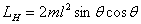 perpendicular
to perpendicular
to  (see
figure 2). (see
figure 2).
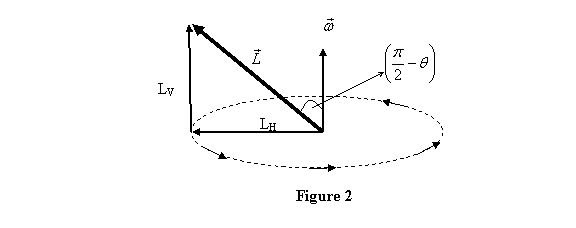
As
the rod rotates LV remains unchanged
but LH sweeps a circle with
angular frequency  .
The rate of change of .
The rate of change of 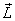 is
therefore the same as that of LH .
The magnitude of the latter is ωLH . Since
at the position shown, the tip of LH is
moving out of the paper, the direction of the change
in LH is
also the same. This is the direction of principal
axis 3. It thus follows that is
therefore the same as that of LH .
The magnitude of the latter is ωLH . Since
at the position shown, the tip of LH is
moving out of the paper, the direction of the change
in LH is
also the same. This is the direction of principal
axis 3. It thus follows that
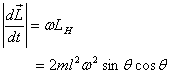
in the direction of principal axis 3. For completeness
I also calculate the kinetic energy of the rod-mass system.
It is
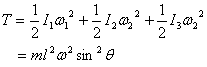
I now give you a couple of exercises similar to the problem
above.
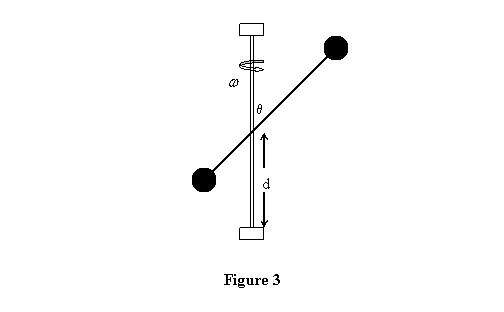
Exercise 1: In the problem above,
if the axis of rotation passes through a different
point than the centre of the rod (see figure 3),
what will be the forces applied by the bearings with
everything else remaining the same? ( Hint: the
CM is now moving in a circle )
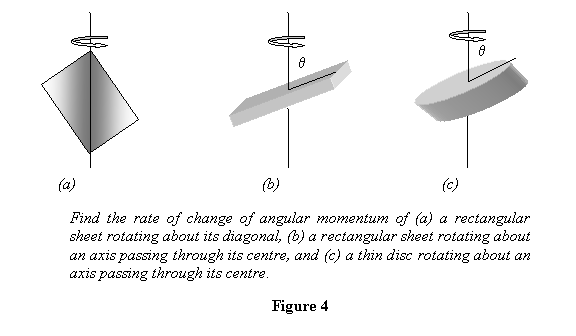
Exercise 2: For the rotating objects
shown below in figure 4, calculate the rate of change
of their angular momentum by the two methods employed
in the example above.
If you have followed the example above, and have also
done the exercises suggested, then you will be in a position
to understand the explanation of two of the three observations
I started my previous lecture with. The two observations
were the precession of a spinning top and only one roller
of the three shown being able to go over a curved track
entirely.
Example 2: Let me take the case of
the precession of a spinning top. In this case we
observe that when a spinning top is put on a floor
and its lower point is held at one point, it starts
precessing about the vertical axis (see figure 5)
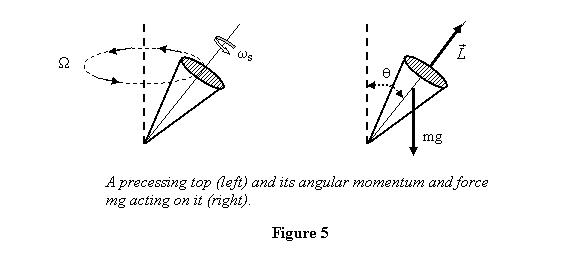
I take the mass of the top to be m, its moment
of inertia about the spinning axis I ,
distance of its CM from the pivot point l and
its spinning rate to be ωs.
The top's axis is making an angle θ from
the vertical. Let us take the rate of precession,
i.e. the angular speed at which the top starts
to rotate about the vertical to be Ω. It
is observed that Ω is usually much smaller
than ωs. So
in calculating angular momentum we are going
to take it as arising from the spin only and
neglect any contribution of Ω to it. The
angular momentum is then along the spin axis
of the top and its magnitude is 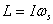 ,
where I is top's moment of inertia
about its axis. Further, there is torque acting
on the top due to its weight. The magnitude of
the torque is mgl sinθ and
it is perpendicular to the plane formed by the
vertical and the spin axis (the direction of ,
where I is top's moment of inertia
about its axis. Further, there is torque acting
on the top due to its weight. The magnitude of
the torque is mgl sinθ and
it is perpendicular to the plane formed by the
vertical and the spin axis (the direction of 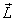 ).
At the position shown in figure 5, the torque
is going into the plane of the paper. The problem
then reduces to the following. A rigid body has
an angular momentum ).
At the position shown in figure 5, the torque
is going into the plane of the paper. The problem
then reduces to the following. A rigid body has
an angular momentum  and
is being acted upon by a torque of magnitude mgl sinθ perpendicular
to and
is being acted upon by a torque of magnitude mgl sinθ perpendicular
to 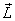 .
What will happen to the body? .
What will happen to the body?
Since the angular momentum is being acted upon by a torque
perpendicular to it, it changes continuously with time
with its magnitude remaining unaffected. Thus it moves
on the surface of a cone as shown in figure 6.
Let me now calculate the frequency of rotation of
vector  .
For this I again look at the vertical LV and
horizontal LH components
of the angular momentum, as shown in figure 6.
The vertical component remains unchanged and
the horizontal component changes at the rate .
For this I again look at the vertical LV and
horizontal LH components
of the angular momentum, as shown in figure 6.
The vertical component remains unchanged and
the horizontal component changes at the rate 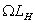 as
the as
the 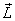 vector
rotates. This gives vector
rotates. This gives 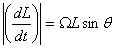 ,
which should be equal to the torque. Substituting ,
which should be equal to the torque. Substituting 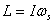 ,
I thus get ,
I thus get
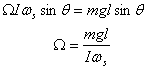
This is the rate at which the 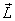 vector
rotates. Since vector
rotates. Since 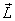 is
attached to the top, the top also rotates at
the same rate. is
attached to the top, the top also rotates at
the same rate. 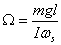 is
then the rate of precession of the cone. is
then the rate of precession of the cone.
As the top precesses, its CM moves in a circle. You
may now wonder where does the centripetal force for
this come from? This is provided by the horizontal
reaction or the frictional force at the pivot point.
Second question you may raise is why is it that the
component LH starts
moving in a horizontal circle due to the torque while
the vertical component does not move in a vertical
circle. In the actual motion, it does. So in addition
to the precession, the axis of the top also oscillates
up and down with very small amplitude. If you are
careful in you observations, you will see this motion.
This is known as the nutation of the top. In our
present treatment, we have ignored this motion and
solved the problem only to get the precession rate.
I now wish to explore if to get this answer, I could equivalently
have used the equations
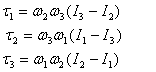
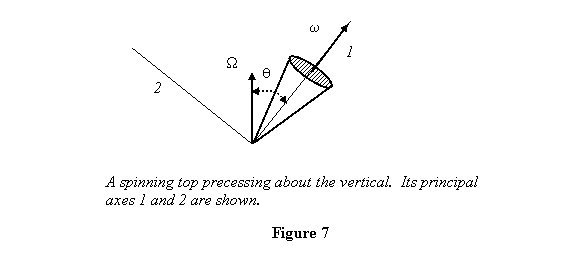
To do this, let me first identify the principal axes of
the cone at the pivot point and label them. The principal
axes are the spin axis and two other axes perpendicular
to it. These are shown and labeled (1,2,3) in
figure 7; in this position axes 1 and 2 are in the plane
of the paper and axis 3 is coming out of it.
The moments of inertia about the principal axes are 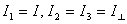 .
The components of .
The components of 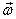 at
the instant (I take it to be time t = 0 )
shown in figure 7 are at
the instant (I take it to be time t = 0 )
shown in figure 7 are
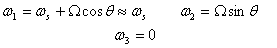
Substituting the values of moments of inertia and the
angular velocity components in the equations for the
components of the torque gives
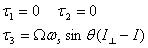
This is not the same answer as obtained earlier. Where
have we gone wrong? Is the previous answer correct
or is this answer correct? We will see later that
in applying the equations above, we have not taken
into account the fact that due to the spin of the
top, its principal axes also spin about axis 1 and
that makes the components of 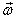 along
them time-dependent. For now I move on to explain
the observation about only one of the rollers being
able to go over all the curves of a track. along
them time-dependent. For now I move on to explain
the observation about only one of the rollers being
able to go over all the curves of a track.
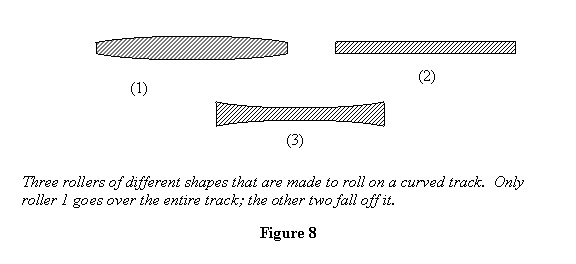
Example 3: If you have performed
the experiment, you would have seen that only roller
1 (see figure 8) that is tapering down as we move
away from its centre is able to go over all the curves.
Let me now explain that.
As a roller goes over a curve, its centre of mass moves
requires a centripetal force to do so. At the same time,
the angular momentum of the roller also changes direction
and that requires a torque. Both the centripetal force
and the torque are provided by the normal reaction of
the track on the rollers. These reaction forces on the
three rollers are shown in figure 9.
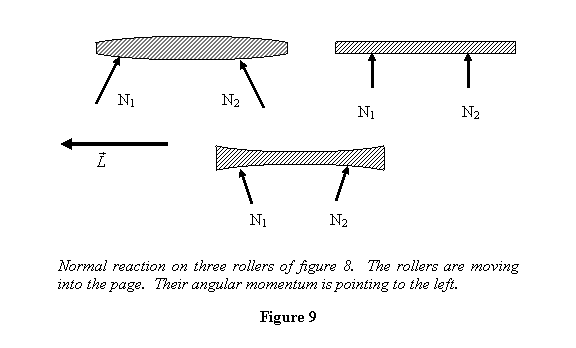
In analyzing the motion of these rollers, I am taking
them to be moving into the paper. Thus the direction
of their angular momentum is to the left, as shown in
the figure. Now if these rollers have to make a turn,
the normal reactions should provide the required centripetal
force in the horizontal direction. This rules out the
plain cylindrical roller (roller 2) from making any turn
because both normal reactions on it are in the vertical
direction. This leaves the other two cylinders for further
consideration. For those rollers, the torque of the normal
reaction forces about the CM should change their angular
momentum vector in the appropriate direction. Let us
look at roller 1 first.
Roller 1: For a left turn, N1 < N2
for centripetal force. Therefore the torque generated
by them is in the direction coming out of the page.
As the roller makes a left turn, the associated change
in its angular momentum also is in the direction
coming out of the page, consistent with the torque
generate. For a right turn by this roller, the centripetal
force is to the right so N1 > N2 .
This generates a torque about the CM that goes into
the page. For the right turn, the change in the angular
momentum is also into the page, consistent with the
torque generated. Thus for roller 1 ,
the centripetal force and the torque generated are
consistent with the centripetal force and the change
in its angular momentum. Let us now see what happens
to roller 3 .
Roller 3: If roller 3 turns left, the centripetal
force will be provided correctly if N1 > N2 .
This however gives a torque about the CM that is
going into the page. On the other hand, during left
turn the change in the angular momentum comes out
of the page. Thus the torque and the change in angular
momentum are in opposite directions. Exactly the
same situation arises for a right turn. Because of
this inconsistency, the roller fails to turn at any
of the curves. This example teaches us about the
centre of mass motion combined with angular momentum
changes about the CM. We now move on to discuss the
general form of the equation relating the torque
and the angular momentum.
|