Lectures 22 & 23
Rotational dynamics V: Kinetic
energy, angular momentum and torque in 3-dimensions
You learnt in the previous lecture is that the angular
velocity 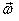 is
a vector quantity pointing in the direction of the
axis of rotation. Any vector that is rotating about is
a vector quantity pointing in the direction of the
axis of rotation. Any vector that is rotating about 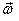 also
changes direction. Thus the vector changes even if
its magnitude is constant. If the vector is also
changes direction. Thus the vector changes even if
its magnitude is constant. If the vector is 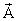 then
its rate of change purely on the basis of rotation
is then
its rate of change purely on the basis of rotation
is
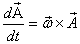
Thus the velocity of a rotating particle at position 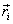 from
the origin is from
the origin is
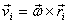
I also derived the general expression for the angular
momentum, which is given as
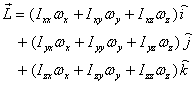
Here 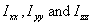 are
the moments of inertia about the x, y and
the z axes, respectively. The off diagonal
elements like Ixy are
the products of inertia. A simplification in
the expression above arises by employing the
principal axes for which the products of inertia
vanish. For convenience in writing, the principal
axes are usually denoted by (1,2,3 )
instead of (x,y,z). Using this notation
the angular momentum vector can be written in
a simple form as are
the moments of inertia about the x, y and
the z axes, respectively. The off diagonal
elements like Ixy are
the products of inertia. A simplification in
the expression above arises by employing the
principal axes for which the products of inertia
vanish. For convenience in writing, the principal
axes are usually denoted by (1,2,3 )
instead of (x,y,z). Using this notation
the angular momentum vector can be written in
a simple form as
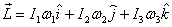
where ω1 , ω2 and ω3 are
the components of the angular velocity along
the principal axes. I now derive the expression
for kinetic energy for a rigid body rotating
with one point fixed.
Kinetic energy of a rotating rigid body: I
consider a rigid body rotating with angular velocity 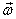 .
Its kinetic energy T is calculated as follows .
Its kinetic energy T is calculated as follows
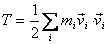
Substituting 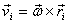 for
of the velocities above and making use of some
identities of vector products we get for
of the velocities above and making use of some
identities of vector products we get

In the principal axes therefore
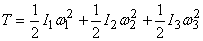
This is the expression for the kinetic energy in terms
of the principal moments of inertia and the components
of angular velocity along the principal set of axes.
Having obtained the general expressions for the angular
momentum and kinetic energy of a rigid body, we now study
the dynamics of a rigid body through the angular-momentum
torque equation. Along the way I will explain the three
observations that I had started my previous lecture with.
Dynamics of a rigid body: Dynamics of
a rigid body is governed by the equation
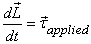
and it is this equation that governs everything about
the rigid-body rotation. What makes the motion
of a rigid-body interesting is that there is a fantastic
interplay between the angular momentum, angular velocity
of a rigid body with or without an applied torque.
For example if the angular velocity and the angular
momentum of a rigid body are not parallel, the 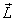 vector
would rotate about vector
would rotate about 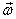 and
that would make and
that would make 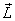 change.
However, if there is no torque applied on the
body, angular momentum cannot change. Therefore
to compensate the change in change.
However, if there is no torque applied on the
body, angular momentum cannot change. Therefore
to compensate the change in 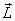 arising
from its rotation, the angular velocity arising
from its rotation, the angular velocity 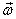 itself
must change. Changing itself
must change. Changing 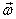 would
make body rotate in a different way and this
goes on. It is thus this interplay between would
make body rotate in a different way and this
goes on. It is thus this interplay between 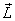 and and 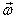 that
makes a rigid body move in seemingly counterintuitive
ways. that
makes a rigid body move in seemingly counterintuitive
ways.
As a body rotates, its angular momentum changes on
two counts: first because in general 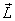 and and 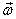 are
not parallel and therefore are
not parallel and therefore 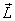 rotates
about rotates
about 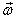 .
With .
With

and
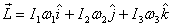
the rate of change of 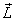 only
due to its rotation about only
due to its rotation about 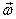 is
given as is
given as
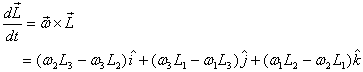
If the components ω1 , ω2 and ω3 were
also changing, I would have to add an additional
term on the right-hand side of the expression above
to take care of that. This is the second reason for
the change in angular momentum of the body. For the
time being I focus on cases where the components
of 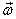 along
the principal axis remain unchanged. This
in turn implies that the magnitude of the angular
momentum remains constant during the rotational motion
of the body. This happens when the applied torque
is always perpendicular to the angular momentum.
Substituting for L1 , L2 and L3 in
the equation above, I get along
the principal axis remain unchanged. This
in turn implies that the magnitude of the angular
momentum remains constant during the rotational motion
of the body. This happens when the applied torque
is always perpendicular to the angular momentum.
Substituting for L1 , L2 and L3 in
the equation above, I get
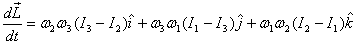
So at any instant the components of 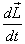 are are
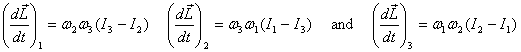
For a geometric interpretation of these equations I urge
you to go back to the previous lecture and see how we
obtained the changes in the coordinates of the end of
a rod rotating infinitesimally. This gives the components
of the torque required to be
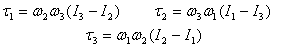
To apply these equations I start with calculation of torque
for the example that we solved at the end of the previous
lecture.
|