Angular momentum of a rigid body rotating with angular velocity 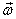: We now derive the relationship between the angular momentum of a body rotating in space with one point fixed. That means the body is not translating and has only three degrees of freedom. By definition, the angular momentum

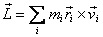
For a rigid body rotating with one point fixed, I have derived above that 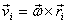. With

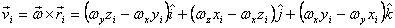
we get

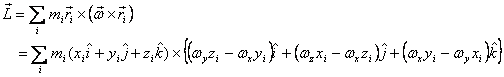
This gives the three components of the angular momentum to be

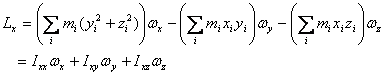
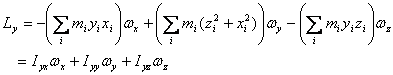
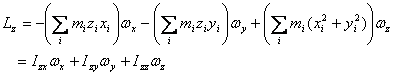
This is usually written in the matrix form

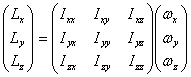
The (3 x 3) matrix in the equation above is known as the moment of inertia tensor. Its diagonal terms

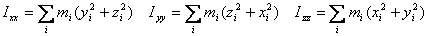
are the moments of inertia about the x , y and the z -axis, respectively. The off-diagonal terms

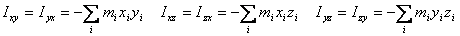
are known as the products of inertia. The values of the moments and products of inertia depend on the set of axes chosen.

So you see that relationship between 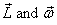is quite involved. Luckily, for a rigid body, for each point one can find a set of axes about so that products of inertia about that point vanish. These are known as the principal axes. Thus for the principal set of axes at a point

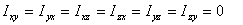
These axes are attached with the body and rotate with it. However, the principal axes offer an advantage when dealing with the angular momentum of a rigid body. At a given time, if I calculate the components of the angular momentum by taking the rigid-body to be rotating in the principal axes frame at that instant, they turn out to be simply L_x =I_xx ω_x , L_y =I_yy ω_y and L_z =I_zz ω_z . Thus the angular momentum of the body is given as

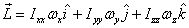
at any given instant. It is easily seen from the expression above that in general the angular momentum and the angular velocity are not parallel; they will be parallel only if 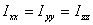, i.e. if all three moments of inertia about the principal axes are equal. This is shown in figure 8 in two dimensions.

Let me now solve an example.

 

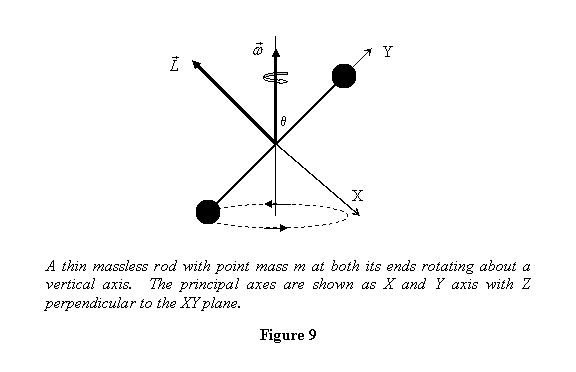
Example 2: A thin massless rod of length 2l has a point mass m at both its ends. It is rotating with angular speed w about a vertical axis passing through its centre and at an angle θ from it, as shown in figure 9. Calculate its angular momentum.

 

We will apply the formula for angular momentum derived above. It is easy to see that at the centre of the rod, the principal axes are: one axis parallel to the rod and two of them perpendicular to it. These are shown in the figure above. Notice that the principal axes rotate with the body. The moment of inertia with respect to the principal axes shown in figure 9 are

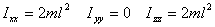
The components of the angular velocity along the principal axes are

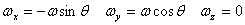
Thus the angular momentum is given as

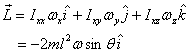
This is also shown in figure 9. It is clear from the figure that as the body rotates so does its angular momentum vector. Thus the angular momentum of the body changes with time although its magnitude remains unchanged.

I end this lecture by asking you to solve a similar problem.

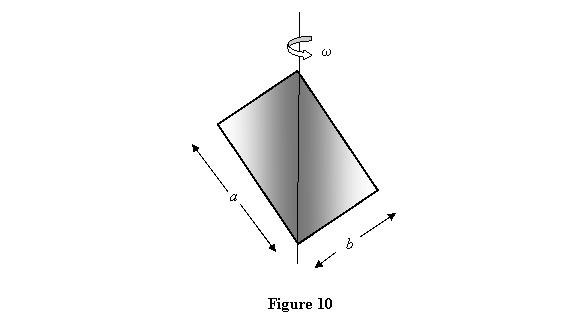
Exercise: A rectangular thin sheet of sides a and b is rotating about one of its diagonals (see figure 10) with angular speed ω. The mass of the sheet is m. What is its angular momentum? Express it in terms of the principal axes unit vectors.