Let me again take a rod lying along the x-axis
with one end fixed at the origin and
the other at (l,0,0).
However, this time I consider infinitesimal
rotations about the y and the z axes.
I do so because I want both the rotations
to cause change in the orientation of
the rod; first rotation about the x-axis
does not do that. Before I present the
calculations, I would like you to recall
from the first lecture how different
components of a vector change when the
frame is rotated. I would be making use
of those relationships now with one change:
rotating a vector by an angle Δθ about
an axis is same as viewing it from
a frame rotated by the angle -Δθ about
the same axis. I perform a rotation of
the rod about the y-axis by an angle Δθy and
that about the z-axis by angle Δθz.
Let me first consider the case of
rotation about the y-axis that is
followed by a rotation about the
z-axis. Rotation of the rod about
the y-axis gives the new coordinates
of it free end as
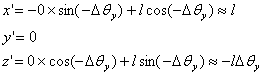
Now rotate the rod about z-axis to get coordinates of
its free end as
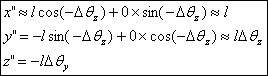
Let us now do it the other way. Rotation about the z-axis
gives
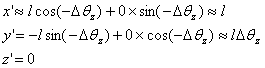
Now give a rotation about the y-axis to get
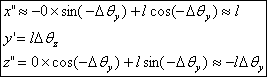
When we compare the two boxed results above, we
find that the coordinates of the end point of
the rod come out to be the same. We conclude
that two infinitesimal rotations will give the
same final result irrespective of the order in
which they are applied. Thus infinitesimal
rotations can be treated as vectors . But
what about the direction of rotation? To assign
a direction, notice that the change in the position
vector 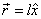 of
the end coordinate of the rod considered
above can be written as
of
the end coordinate of the rod considered
above can be written as
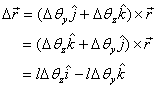
where I have written the second line above to
emphasize that the order in which infinitesimal
rotations are performed does not affect the end
result of these operations. The equations above
suggest that an infinitesimal rotation about
an axis be assigned a direction parallel to the
axis following the right hand convention:
If the thumb of the right hand points in the
direction of the infinitesimal rotation, the
movement of fingers gives the sense of rotation.
With this definition, the change in the position
vector of a point after it is rotated
by an infinitesimal angle Δθ about
an axis in the direction of unit vector 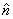 (sense
of rotation given by right hand convention)
is given as
(sense
of rotation given by right hand convention)
is given as
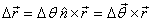
It is obvious that the vector 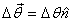 .
The corresponding derivative with respect time is called
the angular velocity, usually denoted by
.
The corresponding derivative with respect time is called
the angular velocity, usually denoted by 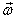 .
Thus
.
Thus
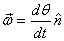
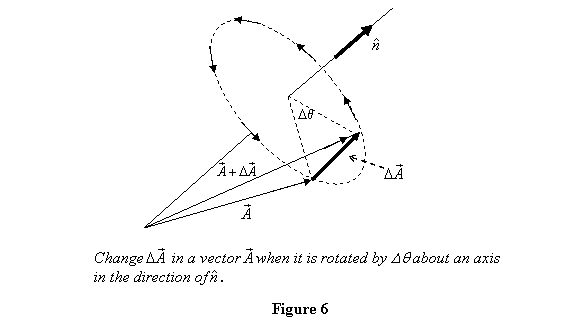
I now point out that although the above equation
is written for a position vector, there is nothing
in its derivation that limits it to position
vectors only. It is in fact true for any vector
as can be easily proved by replacing the (xyz)
coordinates by the corresponding components of
the vector in the derivation above. Thus if a
vector 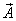 is
given an infinitesimal rotation
is
given an infinitesimal rotation 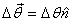 ,
its will change by
,
its will change by
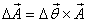
This is shown pictorially in figure 6.
Let us now see how much does a vector  change
when we apply two infinitesimal rotations
change
when we apply two infinitesimal rotations 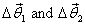 about
two different axes. Let the vector be
denoted by
about
two different axes. Let the vector be
denoted by 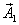 after
the first rotation and by
after
the first rotation and by 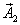 after
the second one. Then we have
after
the second one. Then we have

thereby showing that for several infinitesimal rotations
the final effect can indeed be expressed by adding the
effect of each one of them.
Next we consider the rate of change of a vector rotating
with an angular velocity 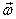 .
It is obtained as follows:
.
It is obtained as follows:
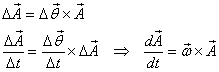
This is the rate of change of a vector  only
due to its rotation. If it changes additionally
due to some other causes, that has to be added
to the above change separately. If we take the
vector
only
due to its rotation. If it changes additionally
due to some other causes, that has to be added
to the above change separately. If we take the
vector  to
be the position vector
to
be the position vector  ,
we get the formula
,
we get the formula
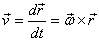
for linear velocity of a particle due to pure rotation
of its position vector.
You may ask this point why is it that we want
to take 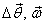 as
vector quantities. The answer is that
we in doing our calculations, we should know
whether a quantity is a scalar or a vector or
something else so that mathematical operations
on it can be appropriately defined. For example,
now that we know that
as
vector quantities. The answer is that
we in doing our calculations, we should know
whether a quantity is a scalar or a vector or
something else so that mathematical operations
on it can be appropriately defined. For example,
now that we know that 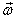 is
a vector quantity, we can take its components
and deal with them independently. Let
me give you an example.
is
a vector quantity, we can take its components
and deal with them independently. Let
me give you an example.
Example 1: A ball is given a
spin at speed w and then put on a rough floor
with 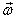 making
an angle q with the vertical. When the
ball eventually rolls, what would be its rolling
speed (see figure 7)?
making
an angle q with the vertical. When the
ball eventually rolls, what would be its rolling
speed (see figure 7)?

In solving this problem, I make use of the vector nature
of 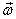 and
split it into its two components. It is the horizontal
component
and
split it into its two components. It is the horizontal
component 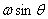 that
is responsible for making the ball roll. The vertical
component
that
is responsible for making the ball roll. The vertical
component 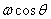 does
not contribute to rolling, as you well know. Further,
this component eventually goes to zero due to friction.
So the question is: if a sphere rotating with angular
speed
does
not contribute to rolling, as you well know. Further,
this component eventually goes to zero due to friction.
So the question is: if a sphere rotating with angular
speed 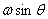 is
kept on a rough floor with axis of rotation horizontal,
what is its find rolling speed. I will let you figure
that out. The point that is emphasized here is that knowing
that
is
kept on a rough floor with axis of rotation horizontal,
what is its find rolling speed. I will let you figure
that out. The point that is emphasized here is that knowing
that 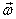 is
a vector quantity helped us to solve the problem easily.
is
a vector quantity helped us to solve the problem easily.
Now that we know 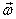 is
a vector, the next question we ask is:
how does
is
a vector, the next question we ask is:
how does 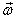 change
when an external torque is applied on
a body? So far we have learnt that external torques
change angular momentum
change
when an external torque is applied on
a body? So far we have learnt that external torques
change angular momentum 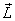 .
So to know how
.
So to know how 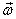 changes,
we should know the relationship between
changes,
we should know the relationship between 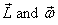 .
We derive this relationship next.
.
We derive this relationship next.