Lecture 21
Rotational dynamics IV: Angular velocity and angular momentum

In the previous three lectures, we have dealt primarily with rotation about a fixed axis or an axis moving parallel to itself. What we saw in those lectures was that dynamics of a rigid body is described by 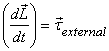and in the absence of 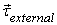the angular momentum 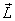is a conserved. In the case of fixed axis rotation, the relationship between the angular momentum and the angular speed was quite straight forward in that 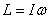and all that was done in those problems was to change the magnitude of ω to change L. But the rotational motion is much more interesting than that. For example is a vector so it could change direction because of applied torque with or without its magnitude being affected. How the changing direction of affects the orientation of a rigid body is one question we should answer if we wish to understand the motion of a rigid body. To start with, I want to point out to you that rotational motion is sometimes not what one would expect naively.

You must have played with a top. If it is not spinning and we try to make it stand on its pivot, it falls sideways. On the other hand, if it is given a spin and then put on its pivot point, it does not fall but starts to move about, what is called precession, a vertical axis passing through its pivot point. This is shown in figure 1. Obviously the precession of the top has something to do with its spin.

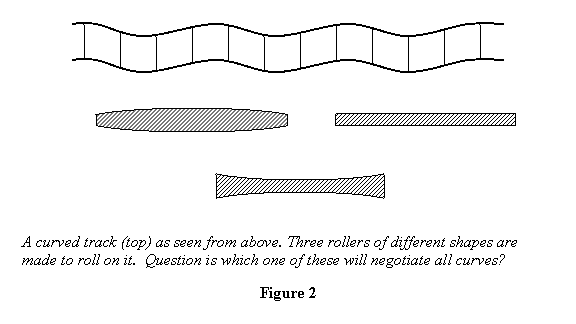
My second observation is from something that is seen in science museums. You can also make it easily in your local workshop. Take a track with many soft curves on it and let three different shape rollers roll on it. You may want to keep the track slightly tilted so that the rollers roll by themselves. Question is which of the rollers will be able to negotiate all the curves.

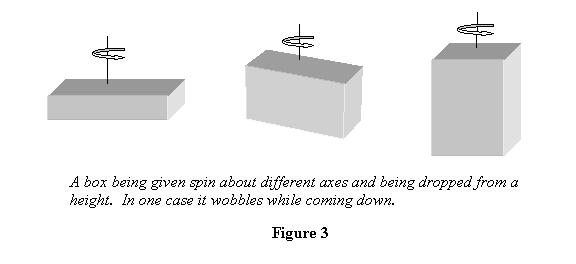
I make the third observation on a rectangular box of sweets (empty of course) or any similar box. Put a rubber-band around it so that its lid does not come off. Hold the box at a height with one of its faces perpendicular to the vertical, give it a spin and let it drop (see figure 3). Observe how its spin changes when it is falling down. You will find that in two out of three possible ways of holding the box, its spin will remain essentially unchanged whereas in one case it will start wobbling. On the other hand, if the box is dropped without giving it a spin, it comes down in the same orientation. What does the spin do to it? We wish to understand this.

In all three cases we see that when an object is given a spin its motion is very different compared to when it is not spinning. This happens because the angular momentum of the object due to its spin changes direction during the motion and the orientation of the body changes accordingly. So we now really have to get into the vector nature of angular momentum and relate it to the parameters - the angle and the angular speed / velocity - of the body. I develop this structure of three-dimensional rigid-body dynamics step-by-step. The first question we address in this development is if the angle of rotation θ can be expressed as a vector 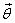? And if the answer is yes, what is its direction?

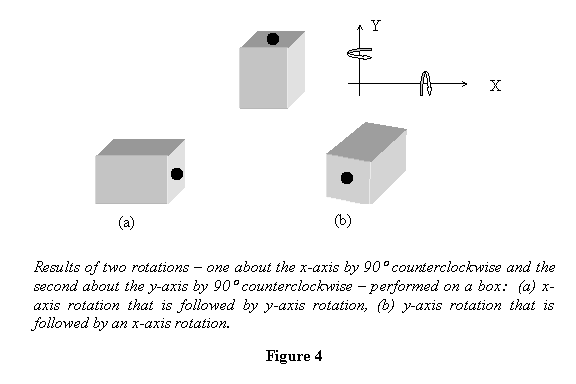
The answer to the question whether an angle of rotation can be treated as a vector is in the negative. This is because it fails to satisfy a fundamental property - that the addition of vectors is commutative - of vector addition. Thus if we make two rotations of angles θ₁ and θ₂ about two different axes, the end results will not be the same if the order of rotations is changed. This is depicted in figure 4 where I show a rectangular box that is to be rotated by 90° about the x and the y axes. The x and y axes are in the plane of the paper and pass through the centre of the box; the z-axis is coming out of the paper. The results are different if (a) I do the rotation about the x-axis first and then follow it with a rotation about the y-axis, and (b) I do the rotation about the y-axis first and then follow it with a rotation about the x-axis. Thus θ₁ and θ₂ cannot be treated as vectors because .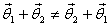

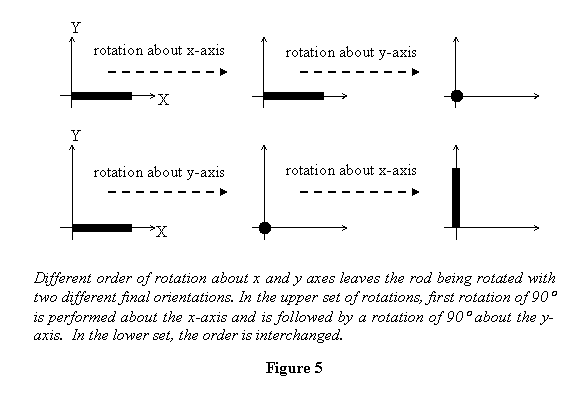
Mathematically let us take a rod of length l lying along the x-axis with one of its ends at the origin so that the (xyz) coordinates of its other end are (l, 0, 0). Keeping its end at the origin fixed, the rod is rotated about the x and the y axes in the same manner as the box in figure 4. If rotated about the x-axis first the end still has coordinates (l, 0, 0). Now the rotation about the y-axis makes the rod align with the z-axis with the new coordinates of its end being (0, 0, - l) . Let us perform the rotations in the other order now. The first rotation is performed about the y-axis and makes the rod align with the z-axis with the new coordinates of its end being rod (0, 0, - l) . Now the rotation about the x-axis makes the rod align with the y-axis and the final coordinates of its end are (0, l, 0) . Thus we see that two rotations have absolutely different effect on the orientation of a body depending on their order. This is demonstrated in figure 5. The conclusion therefore is that rotations in general cannot be treated as vectors .

Although rotations by a finite angle are no vector quantities, rotations by infinitesimal angles Δθ are. This also makes the derivative 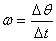a vector quantity. We therefore call this quantity angular velocity rather than angular speed. Let me first show you through a simple example that infinitesimal rotations do satisfy the commutative property of vector addition and then go on to assign a direction to such rotations.